9. Relations

CAUTION - CHAPTER UNDER CONSTRUCTION!

NOTICE: If you are NOT enrolled in the CSC 230 course that I teach at SFSU, you probably are looking for the “public version” of the book, which I only update between semesters. The version you are looking at now is the “CSC230 version” of the book, which I will be updating throughout the semester.

This chapter was last updated on October 20, 2025.
Revised the sections/subsections on partial orders, well-ordering, and modular arithmetic.
Made other minor revisions and fixed typos.

Relations are used to describe an association of data.

For example, imagine a university database of students. The database needs to have a record for each student, and the student’s record needs to include fields for the student’s name(s), the unique student ID number for the student, the student’s current status, a list of courses that the student has enrolled in or has completed (along with the grade earned in each completed course,) and possibly other data associated with the student. One way to visualize the database is as a two-dimensional table, similar to a spreadsheet worksheet, where each row corresponds to a record and each column corresponds to a field; each row can be treated as an ordered \(n\)-tuple, where \(n\) is the number of fields.

In this chapter, you will learn about the formal definition of relation, operations and properties of relations. You will also learn about some special types of relations, namely partial orderings and equivalence relations. As a special case of equivalence relations, you will learn about congruence relations of integers as well as modular arithmetic.

Key terms and concepts covered in this chapter:

  • Relations

  • Properties of relations (reflexivity, symmetry, transitivity, and other properties)

  • Equivalence relations

    • Equivalence classes

  • Modular arithmetic

    • Congruences

  • Partial orders

  • Well orderings

9.1. Definition of Relation

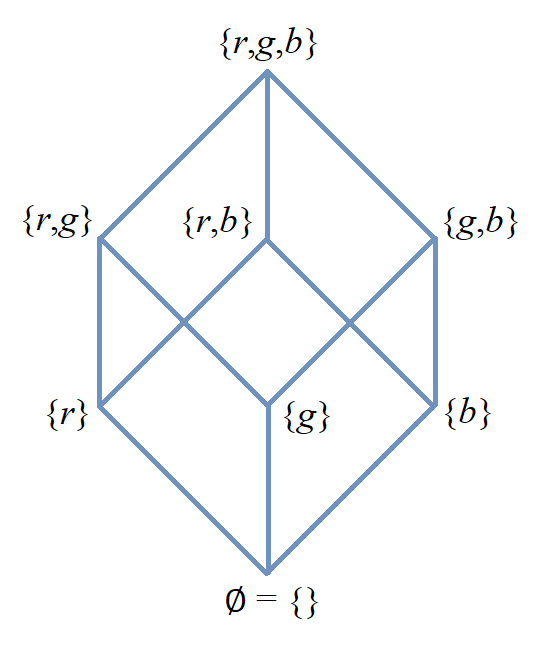
Informally, a relation on two or more sets is an association between elements of those sets. Formally, a relation is a subset of a Cartesian product of two or more sets.
For simplicity, it is assumed in this textbook that the number of sets used to form the Cartesian product is finite. It is possible to define relations as subsets of a Cartesian product of infinitely many sets, in which case the elements of the relation are infinite sequences.

Definition

An n -ary relation on the sets \(A_{1}, \, A_{2}, \, \ldots \, A_{n},\) where \(n \geq 2\) is a natural number, is a subset \(R\) of the Cartesian product \(A_{1} \times A_{2} \times \cdots \times A_{n}.\) That is, any subset \(R \subseteq A_{1} \times A_{2} \times \cdots \times A_{n}\) is a n -ary relation on the sets \(A_{1}, \, A_{2}, \, \ldots \, A_{n}.\)

The sets \(A_{1}, \, A_{2}, \, \ldots \, A_{n}\) are called the domains of the relation \(R.\)

The number of sets \(n\) is called the degree of the relation \(R.\)

Here are several examples of relations.

Example 1 - Relations

  • Let \(A\) be the set of names of students currently enrolled at a college, \(B\) be the set of all possible student ID numbers, and \(C\) be the set of all classes currently offered at the college. The set \[ R = \{ (x, y, z) \mid \text{Student } x \text{ has ID number } y \text{ and is enrolled in class } z \} \] is a 3-ary relation, also called a ternary relation, on \(A,\) \(B,\) and \(C.\)

  • Let \(S\) be the set of names of students currently enrolled at a college. The set \[ R = \{ (x, y) \mid \text{Student } x \text{ is enrolled in a class section in which student } y \text{ also is enrolled} \} \] is a 2-ary relation, usually called a binary relation on \(A\) (since the two sets in \(A \times A\) are the same set.) Most of the focus of this chapter will be on binary relations.

  • Let \(f : A \rightarrow B\) be any function, as defined formally in the Functions chapter. Recall that part of the formal definition states that \(f\) is a subset of \(A \times B,\) so the set \(f\) is a binary relation on the domains \(A\) and \(B.\)

Notice that for any sets \(A_{1}, \, A_{2}, \, \ldots \, A_{n},\) where \(n \geq 2\) is a natural number, we always have the following two relations:

  • \(\emptyset,\) called the empty relation. This relation is also called the void relation and trivial relation in other sources.

  • \(A_{1} \times A_{2} \times \cdots \times A_{n},\) called the universal relation.

9.2. Binary Relations on a Single Set

In many cases, the two domains of a binary relation are the same set; for example, the relation may involve comparing two elements of a set S in some way. In this case, the domain \(S\) is mentioned only once: A binary relation on set S is any subset \(R\) of the cartesian product \(S \times S\), that is, \(R \subseteq S \times S.\)

In the case of a binary relation on \(S,\) we often write \(aRb\) to mean the same thing as \((a,b) \in R.\) This notation may make more sense after reading the following example.

Example 2 - Binary Relations on a Set

Here are some examples of binary relations on one set.

  • \(R = \{ (x, y) \in \mathbb{R} \times \mathbb{R} \, | \, x \leq y \}\). \(R\) is a binary relation on \(\mathbb{R}.\) We write \(x \leq y\) instead of \((x,y) \in R\) (Notice that in this case, we are writing \(xRy\) but replacing the \(R\) by the symbol \(\leq.\))

  • \(D = \{ (a, b) \in \mathbb{Z} \times \mathbb{Z} \, | \, a \text{ is a divisor of } b \}\). \(D\) is a binary relation on \(\mathbb{Z}.\) In this case, we often write \(a | b\) instead of \((a,b) \in D.\) You may not be surprised to learn that this relation is called the divisibility relation on the integers.

  • \(M = \{ (a, b) \in \mathbb{Z} \times \mathbb{Z} \, | \, 2 \text{ is a divisor of } (a-b) \}\). \(M\) is a binary relation on \(\mathbb{Z},\) called congruence modulo 2. This textbook uses the common but nonstandard notation \(a \equiv_{2} b\) instead of \((a,b) \in M.\)
    Note that the ISO standard notation for this relation is \(a \equiv b \ \text{mod } 2\) and that other sources use \(a \equiv b \ (\text{mod } 2).\)

  • For a set \(S,\) recall that \(\mathcal{P}(S)\) is the power set of \(S,\) that is, the set whose elements are all possible subsets of \(S.\) Let \(R = \{ (A, B) \in \mathcal{P}(S) \times \mathcal{P}(S) \, | \, A \subseteq B \}.\) \(R\) is a binary relation on \(\mathcal{P}(S),\) and we write \(A \subseteq B\) instead of \((A,B) \in R.\)

  • For a set \(S,\) we can also define a different relation \(R = \{ (A, B) \in \mathcal{P}(S) \times \mathcal{P}(S) \, | \, A \subset B \},\) that is, \(A\) is a proper subset of \(B.\) This relation is also a binary relation on \(\mathcal{P}(S),\) and we write \(A \subset B\) instead of \((A,B) \in R.\)

  • Let \(S\) be any nonempty set. The set \(\mathbf{id}_S = \{ (x, x) \in \mathbb{R} \times \mathbb{R} \, | \, x \in S \}\) is a binary relation on \(S\) which we refer to as the identity relation on \(S\) (Other sources call this the diagonal of \(S,\) or simply the equality relation on \(S.\)) We write \(a=b\) instead of \((a,b) \in \mathbf{id}_S.\)

  • \(L = \{ \text{("rock", "paper"), ("paper", "scissors"), ("scissors", "rock")} \}\) is a binary relation on the set \(\{ \text{"rock", "paper", "scissors"} \}.\) We write \(xLy\) (that is, "\(x\) loses to \(y\)") instead of \((x,y) \in L.\)

9.2.1. Operations on Binary Relations on a Set

Given binary relations \(Q\) and \(R\) on a set \(S,\) we can define several other relations in terms of \(Q\) and \(R.\) These operations are likely familiar to you as operations on functions but they also work for binary relations on a single set.

  • The inverse of \(R\) is the relation \(R^{-1} = \{ (b,a) \, | \, (a,b) \in R \}.\)

  • The composition of Q and R is \(R \circ Q = \{ (a,c) \, | \, (a,b) \in Q \land (b,c) \in R \}.\)

  • The n th power of \(R\) is defined recursively for all \(n \in \mathbb{N}\) as follows.

    • \(R^{0} = \mathbf{id}_S\)

    • \(R^{k+1} = R \circ R^{k}\) for natural numbers \(k > 0.\)
      The recursion step uses \(k\) instead of \(n\) in preparation for the type of arguments used in the chapter on proof by mathematical induction.

Building on the \(n\)th powers of \(R,\) we can define two relations.

  • \(R^{+}\) is the relation \(\{ (a,b) \in S \times S \, | \, (a,b) \in R^{k} \text{ for some positive integer } k \}.\) That is, \(R^{+}\) is the union of all the positive \(n\)th powers of \(R.\)

  • \(R^{*}\) is the relation \(\{ (a,b) \in S \times S \, | \, (a,b) \in R^{k} \text{ for some natural number } k \}.\) That is, \(R^{*}\) is the union of all the natural number \(n\)th powers of \(R.\)

Notice that \(R^{*} = \mathbf{id}_S \cup R^{+}.\)

9.2.2. Properties of Binary Relations on a Set

In this subsection we define five properties that a relation may satisfy.

Definitions

Let \(R\) be a binary relation on the set \(S.\)

  • \(R\) is reflexive if and only if for all \(a \in S,\) \((a, a) \in R.\)

  • \(R\) is irreflexive if and only if for all \(a \in S,\) \((a, a) \not\in R.\)

  • \(R\) is symmetric if and only if for all \(a \in S\) and \(b \in S,\) \((a, b) \in R \rightarrow (b,a) \in R.\)

  • \(R\) is antisymmetric if and only if for all \(a \in S\) and \(b \in S,\) \((a, b) \in R \land (b, a) \in R \rightarrow a = b.\)
    Equivalently, \(R\) is antisymmetric if and only if for all \(a \in S\) and \(b \in S,\) \((a, b) \in R \land a \neq b \rightarrow (b,a) \not\in R.\)

  • \(R\) is transitive if and only if for all \(a \in S,\) \(b \in S,\) and \(c \in S,\) \((a, b) \in R \land (b, c) \in R \rightarrow (a,c) \in R.\)

The following theorem can make it easier to determine when a relationship has each of the five properties. The proof of the theorem is an exercise.

Theorem

Let \(R\) be a binary relation on the set \(S.\)

  • \(R\) is reflexive if and only if \(\mathbf{id}_S \subseteq R.\)

  • \(R\) is irreflexive if and only if \(\mathbf{id}_S \cap R = \emptyset.\)

  • \(R\) is symmetric if and only if \(R^{-1} = R.\)

  • \(R\) is antisymmemtric if and only if \(R^{-1} \cap R \subseteq \mathbf{id}_S.\)

  • \(R\) is transitive if and only if \(R^{2} \subseteq R.\)
    Recall that \(R^{2}\) is defined to be the composition \(R \circ R.\)

9.2.3. Closures of Binary Relations with Respect to a Property

For each of the properties reflexivity, symmetry, and transitivity, we define the closure with respect to the property of a relation \(R\) as follows: The closure is the smallest relation that has the property and includes all the elements of \(R.\) That is, you start with \(R\) and try to insert in just enough ordered pairs, if any are needed, to make sure that the new relation has the desired property.

The following theorem justifies that the reflexive closure, symmetric closure, and transitive closure exist for any relation \(R.\) The proof of the theorem is an exercise.

Theorem

Let \(R\) be a binary relation on the set \(S.\)

  • The reflexive closure of \(R\) is the relation \(R \cup \mathbf{id}_S.\)

  • The symmetric closure of \(R\) is the relation \(R \cup R^{-1}.\)

  • The transitive closure of \(R\) is the relation \(R^{+}.\)

Notice that we can also define the reflexive and transitive closure of a relation \(R\) as the relation \(R^{*},\) which is the reflexive closure of the transitive closure of \(R.\)

However, for some properties, the closure of a relation \(R\) with respect to the property may not exist!

Informal Exercise

The irreflexive closure and antisymmetric closure only exist if \(R\) satisfies certain conditions.

  1. Find a description of the relations \(R\) that do have an irreflexive closure.

  2. Find a description of the relations \(R\) that do have an antisymmetric closure.

Hint
Use the theorem from the previous subsection that describes irreflexive relations and antisymmetric relations in terms of intersections of sets.

9.3. Equivalence Relations

A binary relation \(R\) on a set \(S\) is called an equivalence relation on \(S\) if \(R\) is reflexive, symmetric, and transitive.

A first example of an equivalence relation is the diagonal, that is, the equality relation. Another example is given below.

Example 3 - The Parity Relation on the Integers

Consider the set \(R = \{ (a,b) \in \mathbb{Z} \times \mathbb{Z} \, | \, \text{Both } a \text{ and } b \text{ are odd, or both } a \text{ and } b \text{ are even.} \}.\)

Let’s show that \(R\) is an equivalence relation.

  • \(R\) is reflexive, since \(aRa\) for every \(a \in \mathbb{Z}.\) That is, both \(a\) is odd and \(a\) is odd, or both \(a\) is even and \(a\) is even (since \(p \land p \leftrightarrow p\) is a tautology for any propositional variable \(p.\))

  • \(R\) is symmetric, since \(aRb\) implies \(bRa\) for every pair \(a, b \in \mathbb{Z}.\) That is, both \(a\) and \(b\) are odd whenever both \(b\) and \(a\) are odd, and both \(a\) and \(b\) are even whenever both \(b\) and \(a\) are even (since \(p \land q \leftrightarrow q \land p\) is a tautology for any propositional variables \(p\) and \(q.\))

  • \(R\) is transitive, since \(aRb\) and \(bRc\) implies \(aRc\) for every triple \(a, b, c \in \mathbb{Z}.\) That is, if both \(a\) and \(b\) are odd and both \(b\) and \(c\) are odd, then both \(a\) and \(c\) are odd, and if both \(a\) and \(b\) are even and both \(b\) and \(c\) are even, then both \(a\) and \(c\) are even (since \((p \land q) \land (q \land r) \rightarrow (p \land r)\) is a tautology for any propositional variables \(p,\) \(q,\) and \(r.\))

It is not difficult to see that this relation can also be defined as \(R = \{ (a,b) \in \mathbb{Z} \times \mathbb{Z} \, | \, 2 \text{ is a divisor of } (a-b) \}.\) So this relation is the same as the \(\equiv_{2}\) relation discussed in an earlier example.

Given an equivalence relation \(R\) on the set \(S\) and an element \(x \in S,\) we define the equivalence class of \(x\) to be \([ x ]_{R} = \{ y \in S \, | \, (x,y) \in R \}.\)

Theorem

Let \(R\) be a binary relation on the set \(S.\)

If \(R\) is an equivalence relation then the set of all equivalence classes \(\{ [ x ]_{R} \, | \, x \in S \}\) is a partition of S.

Conversely, if \(\Pi\) is a partition of \(S\), then the relation defined by \(R = \{ (x, y) \, | \, x \text{ and } y \text{ are elements of the same subset in } \Pi \}\) is an equivalence relation.

9.4. Order Relations on a Set

It is often useful to be able to compare elements of a set, based on some key property. In this subsection, several examples of such order relations will be discussed.

9.4.1. Partial Orderings

A binary relation \(R\) on a set \(S\) is called a partial order on \(S\) if \(R\) is reflexive, antisymmetric, and transitive.

Example 4 - Partial Orders

For any set \(S,\) each of the relations \(\subseteq\) and \(\subset\) is a partial order on \(\mathcal{P}(S),\) the power set of \(S.\)

subset_lattice_for_set_with_3_members_v2

As an example, for the set \(S = \{ r, g, b \},\) the image shows a Hasse diagram that represents the \(\subset\) relation on the power set \(\mathcal{P}(S).\) Notice that each line segment in the Hasse diagram connects a first subset of \(S\) to a second subset of \(S\) that is “immediately above” the first subset in the following sense: Each member of the first subset is also a member of the second subset, but the second subset has one additional member. In the Hasse diagram, two different subsets \(A\) and \(B\) satisfy \(A \subset B\) if and only if there is a “path up” from \(A\) to \(B\) that uses one or more of the line segments.

Total Orderings

A total ordering of a set \(S\) is a partial order \(R\) on \(S\) that has the additional property \((\forall x \in S)(\forall y \in S)(xRy \lor yRx).\)

Example 5 - Total Orderings

  • For the set of real numbers \(\mathbb{R}\) the usual order relations \(\leq\) and \(\geq\) are total orders.

Well-Orderings

A well-ordering of a set \(S\) is a total ordering \(R\) on \(S\) that has the additional property that every nonempty subset of \(S\) contains a least element with respect to the order relation.

One of the most important examples of a well-ordering in mathematics is the relation \(\leq\) on the set of natural numbers \(\mathbb{N}.\)

The Well-Ordering Principle for \(\mathbb{N}\)

If \(S\) is a nonempty subset of \(\mathbb{N}\) then there is a natural number \(m \in S\) such that for every element \(x \in S,\) \(m \leq x.\)

In the Remix, the Well-Ordering Principle is treated as an axiom, a statement that is assumed to be True about the set of natural numbers.

Note to instructors - click to expand
Many textbooks assume either the Well-Ordering Principle or the Principle of Mathematical Induction as an axiom, and then prove the other principle using that axiom (and also prove that the two principles are logically equivalent.) As the Remix is designed for students of Computer Science, both principles are simply assumed to be True without proof, that is, both principles are treated as axioms. This choice should not limit student understanding of how these principles can be applied, and also avoids some highly technical issues that arise in formal mathematical definitions of the set \(\mathbb{N}\) of natural numbers which would most likely only be of concern to Mathematics majors and their instructors. If you want to do a deeper mathematical exploration of these technical issues (e.g., differing formulations of the Peano axioms, and first-order versus second-order logic) you may refer to this article in The Mathematical Intelligencer as well as the subsection “Nonstandard models” of this Wikipedia page.

The Well-Ordering Principle may seem like an “obviously True” statement. To understand why mathematicians would make it clear that they are assuming that this principle is True is to understand what “infinity” means.

  • First, suppose that you are told that the subset \(A\) of \(\mathbb{N}\) contains the element 10. You can use a brute‑force method to determine the least element of \(A:\) Just ask the following sequence of 10 questions, in the order shown. \[ \text{“Is 0 in \(A?,\)” “Is 1 in \(A?,\)” \(\ldots\), “Is 9 in \(A?\)”} \] If the answer is “No” to all 10 of these questions, then 10 itself is the least element in \(A\), otherwise, the least number in \(A\) is the first value of \(k\) for which the answer to the question “Is \(k\) in \(A?\)” is “Yes.”

  • Next, suppose that you are given a new set \(S\) and told that the number \(10^{10^{10^{10^{10}}}}\) is in \(S.\) You again could try to use the brute‑force method of asking the sequence of \(10^{10^{10^{10^{10}}}}\) questions: \[ \text{“Is 0 in \(S?,\)” “Is 1 in \(S?,\)” \(\ldots\), “Is \(\left( 10^{10^{10^{10^{10}}}}-1 \right)\) in \(S?\)”} \] but even if it took only 1 nanosecond to ask and answer each question, the integer \(10^{10^{10^{10^{10}}}}\) is greater than the number of nanoseconds estimated for our universe to reach its final energy state! That is, it is possible that the answer to one of these questions is “Yes” but that you would never be able to ask that question before the universe ends! Notice that you can use formal logic to justify that either the answers to all of those questions would be “No” or that at least one of the questions would have the answer “Yes” — asking the sequence of questions would determine the least element in \(S\) if you had time to ask enough of the questions, but you (and humanity itself) may not have that much time. For this reason, mathematicians assume that the least element of the set \(S\) exists.
    Notice that a “timeless being” could know all the answers.

9.5. Modular Arithmetic (Revision in Progress!)

Let \(m\) stand for some positive integer constant that is greater than 1. The relation congruence modulo \(m\) is defined to be \[\{ (a, b) \in \mathbb{Z} \times \mathbb{Z} \, : \, m \text{ divides } (a-b) \}.\] The symbol \(\equiv_{m}\) is used to represent congruence modulo \(m\), so \[a \equiv_{m} b \text{ if and only if } m \text{ divides } (a-b).\]

As an example, \(13 \equiv_{3} 7\) because \(3\) divides \(13-7.\) Another way to see that \(13 \equiv_{3} 7\) is to notice that both \(13\) and \(7\) leave a remainder of \(1\) when divided by \(3\) using integer long division.

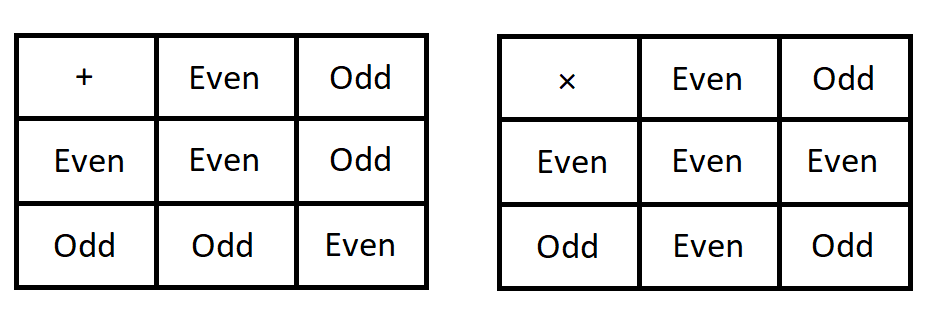
Notice that the relation \(\equiv_{2}\) is the same as the parity relation discussed in an example earlier in this chapter. As discussed in that example, \(\equiv_{2}\) is an equivalence relation. In fact, for each positive integer constant \(m\) that is greater than 1, the relation \(\equiv_{m}\) is an equivalence relation.

Theorem

If \(m\) is a positive integer greater than 1, then \(\equiv_{m}\) is an equivalence relation on \(\mathbb{Z}.\)

Proof

One way to prove this would be to use steps similar to the ones in the parity relation example to show that \(\equiv_{m}\) is reflexive, symmetric, and transitive, but we’ll use a different way to prove this theorem: We will show that the relation \(\equiv_{m}\) describes a way to partition \(\mathbb{Z}\) into \(m\) disjoint subsets, then apply the theorem that states that such a partition corresponds to an equivalence relation.

You’ve already seen how the partition of \(\mathbb{Z}\) into the odd integers and the even integers corresponds to the equivalence relation \(\equiv_{2}.\) Before giving a formal proof, let’s look at another example. If \(m = 3,\) then every integer \(a\) can be written in the form \(a = q \cdot 3 + r\) where \(q\) is an integer and \(r\) is one of the integers in the set \(\{ 0, 1, 2 \}.\) You can partition \(\mathbb{Z}\) into the three subsets listed below: \[\{ \ldots, -3, 0, 3, 6, \ldots \},\] \[\{ \ldots, -2, 1, 4, 7, \ldots \},\] + \[\{ \ldots, -1, 2, 5, 8, \ldots \}.\]

Notice that each integer is in exactly one of those three subsets so the subsets form a partition of \(\mathbb{Z}.\) It’s not difficult to see that two integers are members of the same subset of the partition if and only if \(3\) divides their difference, so the subsets of the partition are the equivalence classes of the relation \(\equiv_{3},\) that is, We will now present the proof for the general case. Notice that if \(a\) is any integer, you can use the division algorithm to find the quotient and remainder such that \(a = q \cdot m + r\), where \(q\) and \(r\) are integers and \(0 \leq r < m.\) This shows that each integer \(a\) is congruent modulo \(m\) to exactly one of the integers in the set \(\{ 0, 1, \ldots, m-1 \},\) which means that the \(m\) sets \[\{ \ldots, -m, 0, m, \ldots \},\] \[\{ \ldots, -m+1, 1, m+1, \ldots \},\] \[\{ \ldots, -m+2, 2, m+2, \ldots \},\] \[ \vdots \] \[\{ \ldots, -2, m-2, m+(m-2), \ldots \},\] \[\{ \ldots, -1, m-1, m+(m-1), \ldots \}\] form a partition of \(\mathbb{Z}.\) By the theorem proved earlier in the chapter, \(\equiv_{m}\) is an equivalence relation with equivalence classes \(\{ [ 0 ]_{\equiv_{m}}, \, [ 1 ]_{\equiv_{m}}, \, [ 2 ]_{\equiv_{m}}, \, \ldots \, [ m-1 ]_{\equiv_{m}} \}\) is the partition of \(\mathbb{Z}\) that corresponds to the relation \(\equiv_{m}.\)

We can also do “arithmetic” directly with the equivalence classes of the \(\equiv_{m}\) relation. The following example may make this more clear.

Example 6 - Arithmetic with Even and Odd Numbers

You likely learned, when you were quite young, that some integers are called "even" and other integers are called "odd."

Notice that every integer is either even or odd but not both, which means that the set \[\{ \text{the set of all even integers}, \, \text{the set of all odd integers} \}\] or more formally \[\{ \{ \ldots, -4, -2, 0, 2, 4, \ldots \}, \, \{ \ldots, -3, -1, 1, 3, \ldots \} \}\]forms a partition of the set \(\mathbb{Z}\) of integers. This partition corresponds to the relation \(\equiv_{2},\) that is, congruence modulo 2. The set of all even numbers is the equivalence class \([ 0 ]_{\equiv_{2}}\) and the set of all odd numbers is the equivalence class \([ 1 ]_{\equiv_{2}}.\)

You may have learned how to do arithmetic with "Even" and "Odd," too, as shown in the tables.

EvenAndOdd

When you did arithmetic with "Even" and "Odd," you were really doing arithmetic with the equivalence classes \([ 0 ]_{\equiv_{2}}\) and \([ 1 ]_{\equiv_{2}}.\) For example, it will not matter which two odd numbers you add, the result must be even because the two numbers were odd. You can just do the operations on the remainders that you get after dividing by 2, which corresponds to adding the equivalence classes: \([ 1 ]_{\equiv_{2}} + [ 1 ]_{\equiv_{2}} = [ 1+1 ]_{\equiv_{2}} = [ 2 ]_{\equiv_{2}} = [ 0 ]_{\equiv_{2}}\) where the last equality is True because \(2\) and \(0\) belong to the same equivalence class (that is, they are both even numbers.)

The following theorem proves that you can do addition and multiplication with the remainders (or, what amounts to the same thing, the equivalence classes) in the same way as was done with Evens and Odds in the previous example for the relation \(\equiv_{m},\) where \(m\) can be any integer greater than 1.

Theorem

If \(m\) is an integer greater than 1, and \(a,\) \(b,\) \(c,\) and \(d\) are integers, and \(a \equiv_{m} b\) and \(c \equiv_{m} d,\)
then \(a + c \equiv_{m} b + d\) and \(a \cdot c \equiv_{m} b \cdot d.\)

Proof

Assume that \(m,\) \(a,\) \(b,\) \(c,\) and \(d\) are integers, \(m > 1,\) \(a \equiv_{m} b,\) and \(c \equiv_{m} d.\) This means that \(m\) is a divisor of both \((a-b)\) and \((c-d),\) that is, both \((a-b)\) and \((c-d)\) are multiples of \(m.\)

The sum \((a-b) + (c-d)\) must also be a multiple of \(m,\) and this sum can be rewritten using properties of addition as \((a+c) - (b+d).\) This shows that \(m\) is a divisor of \((a+c) - (b+d,)\) which can also be stated as \[(a+c) \equiv_{m} (b+d).\]

The expressions \((a-b) \cdot c\) and \(b \cdot (c-d)\) must be multiples of \(m,\) and the sum of those expressions is \((a-b) \cdot c + b \cdot (c-d),\) which can be simplified using properties of multiplication and addition to \((a \cdot c) - (b \cdot d).\) This shows that \(m\) is a divisor of \((a \cdot c) - (b \cdot d),\) which can also be stated as \[(a \cdot c) \equiv_{m} (b \cdot d).\]

Q.E.D.

For example, we can write \(9 + 5 \equiv_{12} 2\) (This is an example of "clock arithmetic" using a 12-hour clock: 5 hours after 9 o’clock will be 2 o’clock.)

Example 7 - Solving a linear congruence

If it is 12 o’clock now, what is the least number of 7-hour intervals that must pass before the clock will read 4 o’clock?

This question is equivalent to finding the smallest natural number \(n\) that solves the linear congruence \(7n \equiv_{12} 4.\)

One way to solve this congruence is to treat this as a "clock arithmetic" problem:
After one 7-hour interval passes, the clock will read 7 o-clock.
After two 7-hour intervals pass, the clock will read 2 o-clock, because \(7+7=14\) and \(14 \equiv_{12} 2.\)
After three 7-hour intervals pass, the clock will read 9 o-clock, because \(2+7 = 9\).
After four 7-hour intervals pass, the clock will read 4 o-clock, because \(9+7 = 16\) and \(16 \equiv_{12} 4.\).
So the least number of 7-hour intervals that must pass before the clock will read 4 o’clock is four.

Another way to solve this congruence is to consider the remainders of natural number-multiples of 7 after dividing by 12:
\(1 \cdot 7 = 7\) and \(7 \equiv_{12} 7\)
\(2 \cdot 7 = 14\) and \(14 \equiv_{12} 2\) since \(14 = 1 \cdot 12 + 2\)
\(3 \cdot 7 = 21\) and \(21 \equiv_{12} 9\) since \(21 = 1 \cdot 12 + 9\)
\(4 \cdot 7 = 28\) and \(28 \equiv_{12} 4\) since \(28 = 2 \cdot 12 + 4\)
Since \(4 \cdot 7 \equiv_{12} 4,\) four 7-hour intervals must pass before the clock will read 4 o’clock.

You try

  • Find the smallest natural number \(n\) such that \(3n \equiv_{11} 5.\)

  • Explain why there is no natural number \(n\) that solves the congruence \(4n \equiv_{10} 5.\)

MORE TO COME!