13. Algorithms and Their Analysis

CAUTION - CHAPTER UNDER CONSTRUCTION!

This chapter was last updated on April 14, 2025.

An algorithm is a step-by-step process, defined by a set of instructions to be executed sequentially, that is used to compute a value or solve a problem. Algorithms are used in discrete mathematics to perform numerical computations, to sort lists, to do searches, insertions, and deletions of items in data structures, to solve optimization problems, and more.
The word algorithm is derived from the name of Abū ‘Abd Allāh Muḥammad ibn Mūsā al-Khwārizmī. Western Europeans learned how to do arithmetic with Hindu-Arabic numerals and the base-ten place-value system from a 12th-century AD Latin translation of one of al-Khwārizmī’s books (The Latin translation was done about 300 years after al-Khwārizmī wrote the original book in Arabic; the original is now lost.) By the way, the word algebra is derived from the title of another one of Al-Khwārizmī’s books.

In this chapter, several algorithms are implemented in Python using non-optimal code to illustrate all steps needed. As mentioned in the About this text chapter, this was a deliberate choice because the code examples are designed for teaching the mathematical concepts and for neither presenting the most efficient implementations nor illustrating the "Pythonic" way of coding. However, a few code examples in this chapter do show how you can complete the same task by using some of Python’s built-in methods.

Key terms and concepts covered in this chapter:

  • Algorithm

    • Properties of an algorithm

  • Types of algorithm

    • Arithmetic

    • Search

    • Sorting

13.1. What Is An Algorithm? What Is Not An Algorithm?

There are several problem-solving strategies that humans use, but not all of these strategies are algorithms.

An algorithm should have the following properties, based on Donald E. Knuth’s description in his famous Art of Computer Programming, The: Volume 1: Fundamental Algorithms, 3rd Edition :

Definiteness

Each step must be precisely defined. The actions taken at each step must be unambiguously specified.

Effectiveness

Each step must be so basic that it can be done exactly and in a finite length of time.

Finiteness

The process must terminate after a finite number of steps (although the number of steps may be a very large natural number.)

Input

Zero or more input quantities are taken from a specified set. Inputs can be introduced before the initial step of the algorithm or dynamically before any later step of the algorithm.

Output

The algorithm produces one or more outputs that have a specified relation to the inputs. Furthermore, the algorithm should produce the correct outputs for each set of inputs.

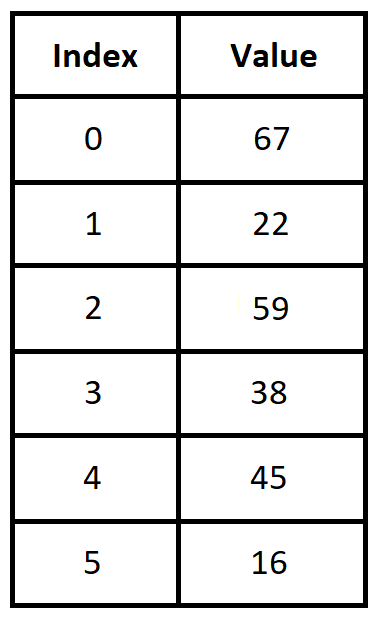
13.1.1. An Example: Finding the Minimum in a List of Integers

Consider the following algorithm for finding the minimum element in a finite sequence of integers.

  • Task: Given a finite list of integers, find then minimum value in the list.

  • Input: A finite list of integers L.

  • Steps:

    1. Define a variable \(min\) and set its value to the initial value in the list.

    2. While there are values in the list that have not been examined,

      1. Increase the index by 1

      2. If the value of the element at the current index is less than the value of \(min,\) set the value of \(min\) to the value of the element at the current index.

  • Output: The value of \(min.\)

Does this satisfy all the requirements for an algorithm? Each step is precisely defined and can be done exactly and in a finite length of time. The process terminates after a finite number of steps (when \(min\) has been compared to the element at the highest index of the list.) The input and output are specified. This process satisfies the requirements for an algorithm.

A Python implementation of this algorithm is given below.

Example 1 - Minimum in Python

The Python code below uses a while loop to implement an algorithm that finds the minimum in a list of integers.

Note that Python provides a built-in function to find the minimum of a list: The minimum value of the list L can be computed using min(L) .

13.2. Arithmetic Algorithms

Historically, algorithms first arose as ways to solve arithmetic problems. In this section, algorithms for such operations are presented.

13.2.1. Division By Repeated Subtraction

A simple division algorithm is presented in this subsection.

Example 2 - Division of Integers by Repeated Subtraction

The code below implements integer division of the positive integer a by the positive integer b. This algorithm is very ancient, dating back to at least Euclid’s Elements.

Click on the "Next" button to step through the code.

Big-O Analysis Of Division By Repeated Subtraction

Notice that the "division by repeated subtraction" algorithm has a worst-case scenario when the divisor b equals 1. In this worst-case scenario you must subtract the divisor \(b=1\) exactly \(a\) times to exit the loop, so "division by repeated subtraction" is \(O(a),\) that is, of at least linear order in the larger number \(a.\)

13.2.2. Long Division Of Natural Numbers

You can revise the previous algorithm to work faster by using place-value thinking.

Example 3 - Long Division

The code below implements integer division of the integer a by the positive integer b.

Click on the "Next" button to step through the code.

This long division algorithm uses powers of two (instead of ten) but otherwise is like the standard algorithm, using decimal notation, that you may have learned in school.
Notice that the shift operators << and >> multiply or divide by 2 ( >> gives only the quotient, without keeping track of the remainder.)

Big-O Analysis Of Long Division

The worst-case scenario corresponds to the divisor \(b=1,\) which requires you to shift as many times as there are binary digits in \(a.\) Notice that \(a\) is bounded above by 2 raised to the number of binary digits; this means that the long division algorithm is \(O(\log (a)).\)

Python provides built-in operators to find the quotient and remainder for variables a and b of type int : a//b is the quotient and a%b is the remainder. There is also the operator divmod(a,b) that returns an ordered pair (of data type tuple ) containing both the quotient and the remainder, but divmod is less efficient than // and % and should only be used when you need to find both the quotient and the remainder.

13.2.3. Greatest Common Divisors: The Euclidean Algorithm

It is often needed to find a common divisor of two integers. This next algorithm goes back to Euclid.

Example 4 - The Euclidean Algorithm

The code below implements integer division for positive integers a and b.

Click on the "Next" button to step through the code.

Big-O Analysis Of The Euclidean Algorithm

The Euclidean Algorithm takes two positive integer inputs \(a\) and \(b\) with \(a > b.\) It can be proven using mathematical induction that the worst-case scenario for this algorithm is \(O(\log (b)).\) The proof uses the closed-form for the Fibonacci numbers.

Python’s math module includes a function gcd that will compute the greatest common divisor of two or more integers.

13.3. Search Algorithms

In the first two subsections you will see two algorithms for searching for a target integer within a list of integers. In the third subsection, Python’s built-in search methods are discussed.

RECOMMENDATION: The "Algorithms and Recursive Functions" activity can replace one or both of the first two subsections.

13.3.1. The Linear Search Algorithm

Linear search compares a target integer, t, to each element in a list of distinct integers, starting at index 0, and returns either the index i at which the target integer was found or a value indicating that the target integer was not found in the list.

A Python implementation of the linear search algorithm is given below.

Example 5 - Linear Search Algorithm in Python

The Python code below uses a while loop to implement the linear search algorithm. The code prints either the index at which the target was found in the list or the built-in constant None to indicate that the target was not found.

Why not use -1 to indicate that the target integer was not found?

Negative integers can be valid indices for a Python list! This is very different than other languages like Java in which indices must be natural numbers. As an example, for the list \(L = \lbrack 2,4,7 \rbrack\) we have \(L \lbrack -1 \rbrack = 7,\) \(L \lbrack -2 \rbrack = 4,\) and \(L \lbrack -3 \rbrack = 2.\) If you are coding in Python it may be safer either to raise an exception or to use the built-in constant None to indicate that no index for the target was found.

Big-O Analysis of Linear Search

The linear search algorithm iterates across a list of \(n\) data elements. If the first element in the list is the target element, the algorithm stops. Otherwise, move to the next element and continue repeatedly until the target element is found or not. If the target element is not in the search list the algorithm exhaustively searches through every single element.

This is the worst case scenario with linear search in which the algorithm inspects every single element, either because the target element is the last element of the array, or the target element is not actually in the search list at all. The algorithm runs in \(O(n)\) time in the worst case.

13.3.2. The Binary Search Algorithm

The binary search algorithm searches a sorted list L of integers for a target value t. The algorithm starts looking for t in the middle of the sorted list. If t is greater than the value in the middle, the algorithm continues the binary search in the upper half of the list, otherwise the algorithm continues the binary search in the lower half of the list. The algorithm continues in this way until we reach a list of length 1 that either does or does not have t as its only element.

Example 6 - Binary Search Algorithm in Python
Big-O Analysis of Binary Search

The binary search algorithm searches for a target element \(x\) in a list of \(n\) elements by comparing the middle element in the the sorted data set with the target \(x\). The algorithm stops if the middle element \(a_m\) is the target element. Otherwise the search continues with half the data set—​the half to the left if the middle element is larger than the target \(x\) or the half to the right if the middle element is smaller than the target.

The number of steps in the binary search then is the number of times we have to split the data set until we locate the target element, or determine that the target element is not in the search list after splitting down to 1 element.

The number of times we need to split the data set of size \(n\), in the worst case then, is \(p\) which is found by solving the exponential equation,

\(2^p = n\).

The algorithm then is \(O(p)\).

The solution of the exponential equation, \(2^p = n\), is in log form,

\(p=\log_2{n}\).

The binary search algorithm then is \(O(p)=O(\log{n})\).

13.3.3. Searching Within a List using Python

In this subsection you will see how to use Python to efficiently search lists.

Example 7 - Searching a List in Python

You can search for the index of a target value in a Python list by calling the list.index(x) method. This method returns the least natural number index of the target value if it is found in the list, otherwise it raises a ValueError.

If you need to know whether the target value x is in the list s but do not need the least index, you can use x in s which returns a Boolean.

If you need to know how many times the target value x occurs in the list s you can use the list.count(x) method.

13.4. Sorting Algorithms

In this section you will see three algorithms for sorting a list of real numbers. Two of these algorithms, bubble sort and insertion sort, are inefficient but are presented here as in many other textbooks because they are easy to understand and analyze. The third algorithm, merge sort, is an efficient recursive algorithm.

In Python, the elements of a list L can be sorted into increasing order by calling the list.sort() method. This built-in method uses one of two sorting algorithms that won’t be discussed in this textbook: the Timsort algorithm in Python versions 2.3 to 3.10, or the Powersort algorithm in Python versions 3.11 to 3.12 (the current version as of this writing).
Python built-in sort() method

The code below uses Python’s built-in sort() method.

13.4.1. Bubble Sort

ArrayWithSixIntegerValues

The bubble sort algorithm is a simple sorting procedure. It is typically used to sort a list of n data elements in either increasing or decreasing order.

NOTE: This algorithm is called "bubble sort" because "the lighter items bubble up to the top" of the list, closer to index 0, like bubbles in a drink.

WARNING: The bubble sort algorithm produces the correct result but is very inefficient. You should almost never use bubble sort in code that you write. In almost every application that requires sorting a list, there is an algorithm that can be used that is much more efficient than bubble sort. You have been warned!
In fact, most modern programming languages have built-in sort methods for you to use; these built-in methods are implemented using efficient algorithms.

We describe the bubble sort algorithm for arranging a list of \(n\) real numbers in increasing order.

  • The algorithm compares the first two elements of the list and swaps them if they are out of order.

  • It continues by traversing the list in order of increasing index, comparing each pair of adjacent elements and swapping them if they are out of order until we reach the last entry in the list at index \(n-1\).

  • The last entry in the list will then be the largest element of the original list.

  • After the largest element has been sorted into position \(n-1\), the algorithm continues by again comparing the first two elements and swapping if they are out of order.

  • Continue traversing the list and comparing and swapping adjacent elements that are out of order until position \(n-2\) of the array, after which the 2nd largest element is at index \(n-2\). The elements, now at indices \(n-1\) and \(n-2\) are sorted.

  • Continue to sort at indices \(n-3,\) then \(n-4,\) and so on, until all elements are in increasing order.

A Python implementation of the bubble sort algorithm is given below.

Python implementation of the Bubble Sort Algorithm

The code below uses two nested while loops to implement the Bubble Sort algorithm.

Big-O Analysis of Bubble Sort

We analyze the bubble sort algorithm beginning with a concrete list of size \(n=5\) and generalize the analysis.

Consider the case of a list of size \(n=5\). The naive bubble sort algorithm in this case will involve 4 passes.

In the first pass, there will be 4 comparisons and up to 4 swaps, after which the element in position 5 is in its correct position.

In the second pass, there will be 3 comparisons and up to 3 swaps, after which the element in position 4 is in its correct position.

In the third pass, there will be 2 comparisons and up to 2 swaps, after which the element in position 3 is in its correct position.

In the fourth pass, there will be 1 comparison and one possible swap , after which both the elements in positions 1 and 2 are both in their correct positions.

Adding the comparisons from each pass we obtain,

\(4+3+2+1=1+2+3+4\).

In general, if the list is of size \(n\), there will be \(n-1\) passes with swaps,

\((n-1)+(n-2)+...+2+1 = 1+2+...+(n-2)+(n-1)\).

You can use mathematical induction to prove that \[1+2+\cdots+(n-2)+(n-1)= \frac{(n-1)\cdot n}{2}\] and since \(\frac{(n-1)\cdot n}{2} =\frac{1}{2}n^2-\frac{1}{2}n\), the bubble sort algorithm is \(O(n^2)\).

13.4.2. Insertion Sort

The insertion sort works through a list and classifies two sections as sorted and unsorted.

  • The insertion sort scans through each element of the list using an outer loop with a variable, say \(i\).

  • At each stage, the list is divided into a sorted section, say the left section, and a section that is not sorted, say the right.

  • The location up to which the list is sorted, is denoted by a pointer or index, called a key.

  • At the current stage, the next element from the unsorted section, on the right, is inserted into its appropriate position in the sorted section on the left.

  • The process of inserting smaller elements in the left involves shifting, larger elements to the right, using a variable, say \(j\).

A Python implementation of the Insertion Sort Algorithm is given below:

Example 8 - Insertion Sort in Python

The code below uses two nested while loops to implement the Insertion Sort algorithm.

Big-O Analysis of Insertion Sort

It is left as an exercise to verify that the insertion sort algorithm is \(O(n^2)\).

13.4.3. Merge Sort

Merge Sort is a recursive sorting algorithm. The general idea is to divide a list of length \(n\) into \(n\) sublists of length \(1\), where a list of length one is considered already sorted. Subsequently, the algorithm repeatedly merges the sublists to make sorted lists until only a single list of length \(n\) is remaining. This will be the a sorted list consisting of the elements of the original list.

The picture below illustrates this with a list of length seven.
Image credit: "Merge Sort Algorithm Diagram" by VineetKumar. This work has been released into the public domain by its author, VineetKumar at English Wikipedia. This applies worldwide.

GGC
Example 9 - The Merge Sort Algorithm in Python
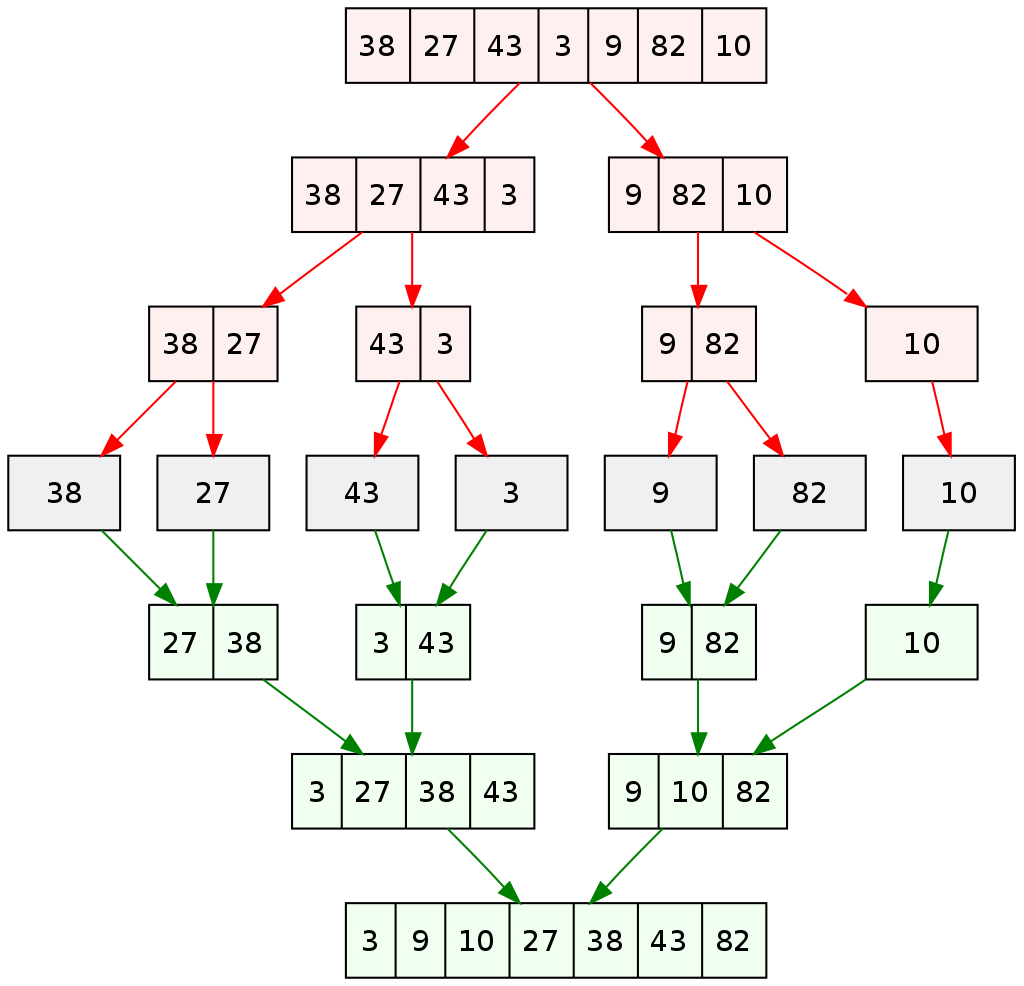
Big-O Analysis of Merge Sort

In the first part of Merge Sort, similar to Binary Search which is \(O(\log{n})\), the list of size \(n\) is recursively split into sublists. In the second part of Merge Sort, \(n\) elements are merged which is \(O(n)\). Since the algorithm performs the first and the second parts, we can multiply to find that the complexity of Merge Sort is \(O(n \log{n})\).

MORE TO COME!