5. Proofs: Basic Techniques

CAUTION - CHAPTER UNDER CONSTRUCTION!

This chapter was last updated on February 25, 2025
Contents locked until 11:59 p.m. Pacific Standard Time on May 23, 2025.

Recall from the Logic chapter that an argument is a finite sequence of statements that ends with a final statement, the conclusion, that is based on inferences made from the earlier statements, called premises or hypotheses.

An argument is valid if it is of a form such that if all premises are True then the conclusion must be True, too. An argument is not valid just because it exists! Just as a proposition is a single statement that may be either True or False (but not both), an argument is a finite sequence of statements that may be either valid or invalid (ut not both.)

A proof is a valid argument made up of propositions. In a proof, some premises may be axioms or postulates, which are propositions that we simply ASSUME to be True. Other premises used in a proof may be previously-proven propositions called theorems. There are many other terms used for theorems depending on the context, such as lemma (a minor theorem needed to prove a more important major theorem) and corollary (a theorem that is a conclusion based on a premise that is a more important theorem), but each of these specialized terms describes a theorem.

Key terms and concepts covered in this chapter:

  • Propositional inference rules (concepts of modus ponens and modus tollens)

    • Notions of implication, equivalence, converse, inverse, contrapositive, negation, and contradiction

  • The structure of mathematical proofs

  • Proof techniques

    • Direct proofs

    • Proof by counterexample (Disproving by counterexample)

    • Proof by contraposition (proof by contrapositive)

    • Proof by contradiction

  • To be added to this chapter after May 23, 2025:

    • logical equivalence and circles of implication

5.1. Rules of Inference for Propositions

To create a proof, we must proceed from True propositions to other True propositions without introducing False propositions into the argument. To do this, we use rules of inference, which are ways to draw a True conclusion from one or more premises that are already known to be True (or assumed to be True). That is, a rule of inference is an argument form that corresponds to a tautology, and so is valid.

Example 1 - Notation For A Rule Of Inference

A rule of inference can be represented as follows.

  • \(p_{1}\)

  • \(p_{2}\)

  • \(\vdots\)

  • \(p_{n}\)

  • \(\therefore q\)

The propositional variables \(p_{1},\,p_{2},\,\ldots,\,p_{n}\) represent the premises of the argument, and \(q\) represents the conclusion of the argument. The symbol \(\therefore\) is read as "therefore".

This rule of inference is interpreted to mean that if all of the propositions \(p_{1},\,p_{2},\,\ldots,\,p_{n}\) are True then the proposition \(q\) MUST be True. The rule of inference in this example corresponds to the tautology \((p_{1} \land p_{2} \land \ldots \land p_{n})\rightarrow q\).

Note that the conclusion \(q\) must be the last proposition, but the order in which the premises \(p_{1},\,p_{2},\,\ldots,\,p_{n}\) are listed in the argument does not matter since we use the conjunction of all premises to prove the conclusion. The premises \(p_{1},\,p_{2},\,\ldots,\,p_{n}\) are usually presented in an order that follows the flow of thought.

Example 2 - Valid and Invalid Arguments

Consider the following three arguments.

A Valid Argument

The following argument was used as an example in the Logic chapter.

  • Sarah earned a B.S. in Computer Science.

  • Anyone who earned a B.S. in Computer Science must have earned a C or better in Discrete Math.

  • Therefore, Sarah earned a C or better in Discrete Math.

The argument is of the form

  • p

  • if p then q

  • \(\therefore\) q

This argument form is named modus ponens which is translated roughly from Latin as "method of affirming". Modus ponens is a valid argument form because it corresponds to the tautology \((p \land (p \rightarrow q)) \rightarrow q\).

\(p\) \(q\) \(p \rightarrow q\) \(p \land (p \rightarrow q)\) \(q\) \((p \land (p \rightarrow q)) \rightarrow q\)

T

T

T

T

T

T

T

F

F

F

F

T

F

T

T

F

T

T

F

F

T

F

F

T

That is, modus ponens is a rule of inference.

An Invalid Argument

Consider this second argument.

  • Arya earned a C or better in Discrete Math.

  • Anyone who earned a B.S. in Computer Science must have earned a C or better in Discrete Math.

  • Therefore, Arya earned a B.S. in Computer Science.

This argument is NOT valid. If we assume that the first two propositions are True, we do not have enough information to reach the conclusion that Arya earned a B.S. in Computer Science: Arya may have earned that degree, or may still be working towards the degree, or may have changed majors and earned a degree in the new major, or perhaps there is some other possibility - we cannot determine whether the conclusion is True or False based on the assumption that the two premises are True.

The argument corresponds to the argument form

  • q

  • if p then q

  • \(\therefore\) p

This argument form is an example of a fallacy or non sequitur , which is Latin for "it does not follow". The argument form is invalid because it corresponds to a proposition that is NOT a tautology, as can be seen in the truth table for the compound proposition \((q \land (p \rightarrow q)) \rightarrow p\).

\(p\) \(q\) \(p \rightarrow q\) \(q \land (p \rightarrow q)\) \(p\) \((q \land (p \rightarrow q)) \rightarrow p\)

T

T

T

T

T

T

T

F

F

F

T

T

F

T

T

T

F

F

F

F

T

F

F

T

Notice that there is at least one row of the truth table in which both \(q\) and \(p \rightarrow q\) are True but \(p\) is False! This means that we can NOT infer that \(p\) is True whenever \((q \land (p \rightarrow q))\) is True. The argument form is invalid because \((q \land (p \rightarrow q)) \rightarrow p\) is not a tautology.

This particular fallacy is used by people so often that it has its own name: The converse error, or fallacy of the converse.

A Third Argument - You Try

Write the argument form for the following argument.

  • Jing did not earn a B.S. in Computer Science.

  • Anyone who earned a B.S. in Computer Science must have earned a C or better in Discrete Math.

  • Therefore, Jing did not earn a C or better in Discrete Math.

Find a compound proposition that corresponds to the argument form you wrote, and write the truth table for that compound proposition.

Question
Is the argument valid?
Hint
The argument is valid if and only if the compound proposition is a tautology.
Answer
No. The argument is invalid and is an example of the inverse error or fallacy of the inverse.

Another way to see that this argument is invalid is to consider a case where Jing did earn a C or better in Discrete Math even though the two premises are True; for example, Jing could have earned a B.S. in Mathematics instead of Computer Science and also earned a C or better in Discrete Math.

In the following subsections we will discuss some of the more common rules of inference.

5.1.1. Transitivity Of The Conditional

The following rule of inference is called pure hypothetical syllogism, but we will use the less formal name transitivity. It is the basis of conditional proof in mathematics.

Transitivity (Pure Hypothetical Syllogism)

  • \(p \rightarrow q\)

  • \(q \rightarrow r\)

  • \(\therefore p \rightarrow r\)

This rule of inference corresponds to the tautology \(((p \rightarrow q) \land (q \rightarrow r)) \rightarrow (p \rightarrow r)\).

By applying transitivity multiple times, you can build a finite chain of implications of any length you want:

  • \(p \rightarrow p_{1}\)

  • \(p_{1} \rightarrow p_{2}\)

  • \(p_{2} \rightarrow p_{3}\)

  • \(\vdots\)

  • \(p_{k-1} \rightarrow p_{k}\)

  • \(p_{k} \rightarrow r\)

  • \(\therefore p \rightarrow r\)

5.1.2. Rules Of Inference And Fallacies Arising From The Conditional

Recall that if you have propositions \(p\) and \(q,\) you can form the conditional with hypothesis \(p\) and consequent \(q,\) which is written as \(p \rightarrow q\), as well as three other related conditionals.

  • \(p \rightarrow q\), the conditional

  • \(q \rightarrow p\), the converse of \(p \rightarrow q\)

  • \(\neg q \rightarrow \neg p\), the contrapositive of \(p \rightarrow q\)

  • \(\neg p \rightarrow \neg q\), the inverse of \(p \rightarrow q\)

Also, recall that \((p \rightarrow q) \equiv (\neg q \rightarrow \neg p)\). That is, \((p \rightarrow q) \leftrightarrow (\neg q \rightarrow \neg p)\) is a tautology. This means that the conditional is logically equivalent to its contrapositive. The conditional is NOT logically equivalent to either its converse or its inverse, as was shown using truth tables in the Logic chapter.

From the four conditionals you can get two rules of inference and two fallacies. Together, these four argument forms are referred to as the mixed hypothetical syllogisms.

First, here are the two rules of inference.

Modus Ponens ("Method Of Affirming")

  • \(p \rightarrow q\)

  • \(p\)

  • \(\therefore q\)

This rule of inference corresponds to the tautology \(((p \rightarrow q) \land p) \rightarrow q\).

Modus Tollens ("Method Of Denying")

  • \(p \rightarrow q\)

  • \(\neg q\)

  • \(\therefore \neg p\)

This rule of inference corresponds to the tautology \(((p \rightarrow q) \land \neg q) \rightarrow \neg p\).

This rule of inference corresponds to replacing the conditional \(p \rightarrow q\) by its logically equivalent contrapositive \(\neg q \rightarrow \neg p\) in the tautology, which gives \(((\neg q \rightarrow \neg p) \land \neg q) \rightarrow \neg p,\) then applying modus ponens to this new tautology.

Next, here are the two fallacies. They are included because they are very common errors to be aware of and to avoid.

Inverse Error

  • \(p \rightarrow q\)

  • \(\neg p\)

  • ∴¬ q

This fallacy arises by mistakenly treating the inverse \(\neg p \rightarrow \neg q\) as if it were logically equivalent to \(p \rightarrow q\). It is also called the "fallacy of the inverse" and "fallacy of denying the hypothesis".

Converse Error

  • \(p \rightarrow q\)

  • \(q\)

  • ∴ p

This fallacy arises by mistakenly treating the converse \(q \rightarrow p\) as if it were logically equivalent to \(p \rightarrow q\). It is also called the "fallacy of the converse" and the "fallacy of affirming the consequent".

The following image uses an Euler diagram of two sets \(A \subseteq B\) to explain why the converse error is a fallacy. The image can also be used to explain why the inverse error is a fallacy.

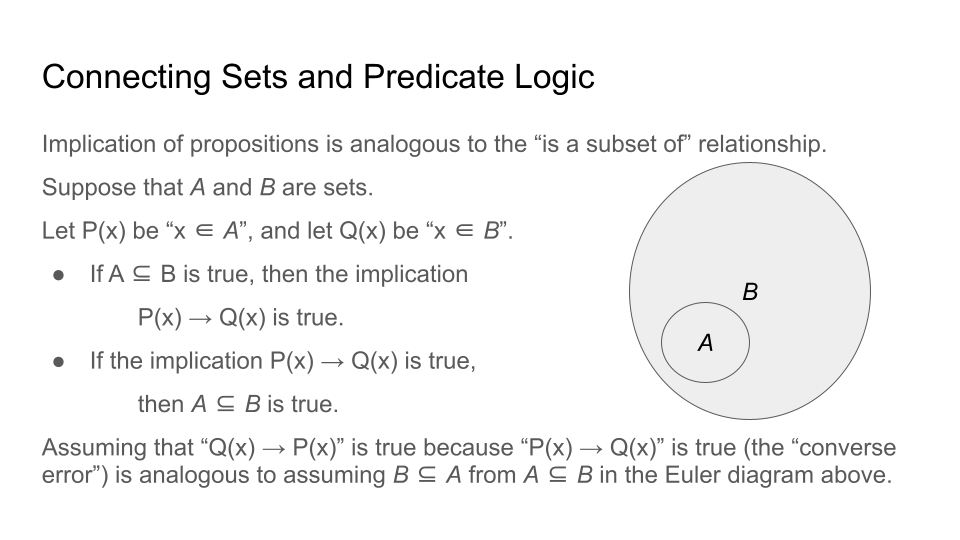
ConverseErrorForSets

Suppose you were told that \(c\) is an element of \(B\) in the preceding image. Can you determine whether \(c\) is an element of \(A\), too?

5.1.3. Other Common Rules Of Inference

Any tautology of the form \(p \rightarrow q\) can be used to define a rule of inference. In particular, we can define a rule of inference corresponding to the tautology \((p_{1} \land p_{2} \land \ldots \land p_{n})\rightarrow p_{1}\) for each integer \(n \geq 1\). This means that there are at least as many possible tautologies as there are natural numbers! How do we deal with infinitely many tautologies?

In general, there is a small number of rules of inference that are used in most proofs. Proofs often are built up to a large size by applying just a few rules of inference multiple times.

Here are some of the more commonly-used rules of inference. In the remix author’s opinion, it’s better to practice using these rules of inference rather than to focus on memorizing them as formal rules with special names.

Proof by Cases

  • \(p \rightarrow r\)

  • \(q \rightarrow r\)

  • \(p \lor q\)

  • \(\therefore r\)

This rule of inference corresponds to the tautology \(((p \rightarrow q) \land (q \rightarrow r) \land (p \lor q)) \rightarrow r\).

Elimination (Disjunctive Syllogism)

  • \(p \lor q\)

  • \(\neg q\)

  • \(\therefore p\)

This rule of inference corresponds to the tautology \(((p \lor q) \land \neg q) \rightarrow p\).

Resolution

  • \(p \rightarrow q\)

  • \(\neg p \rightarrow r\)

  • \(\therefore q \lor r\)

This rule of inference corresponds to the tautology \(((p \rightarrow q) \land (\neg p \rightarrow r)) \rightarrow (q \lor r)\).

Notice that this rule of inference can also be written as
\(\neg p \lor q\)
\(p \lor r\)
\(\therefore q \lor r\)
This form of resolution is important to automated theorem-proving.

Contradiction Rule

  • \(\neg p \rightarrow (q \land \neg q)\)

  • \(\therefore p\)

This rule of inference corresponds to the tautology \((\neg p \rightarrow (q \land \neg q)) \rightarrow p\).

Note that this tautology is often written in the alternate form \(((\neg p \rightarrow q) \land (\neg p \rightarrow \neg q)) \rightarrow p\), which can be more useful in some contexts.

There are many more rules of inference we could write down and give names to. Instead, we’ll just list a few tautologies.

You Try

For each of the tautologies shown, write the argument form for the corresponding rule of inference. If needed, refer to Example 2 in this chapter to see how the argument, argument form, and tautology are related.

  • \((p \land q) \rightarrow p\)

  • \(p \rightarrow (p \lor q)\)

  • \(p \rightarrow (q \rightarrow (p \land q))\)

5.2. Rules Of Inference for Quantified Statements

In this section, four rules of inference that apply to quantified predicates are presented. In all of these rules of inference, the values of the variable(s) are assumed to be restricted to a universal set \(U.\)

5.2.1. Rules of Inference for Universally-Quantified Predicates

Universal instantiation states that, from the premise that \(\forall x P(x)\) is True, where \(x\) ranges over all elements of the universal set \(U,\) you can conclude that \(P(c)\) must also be True, where \(c \in U\) is any arbitrarily-chosen element of \(U.\)

Universal Instantiation (Universal Specification)

  • \(\forall x P(x)\)

  • \(\therefore P(c) \text{ for any } c \in U\)

Universal generalization states that, from the premise that \(P(x)\) is True for every arbitrarily-chosen value of \(x\) that is an element of the universal set \(U,\) you can conclude \(\forall x P(x)\) must also be True, where \(x\) ranges over all elements of the universal set \(U.\)

Universal Generalization

  • \(P(c) \text{ for every } c \in U\)

  • \(\therefore \forall x P(x)\)

You will see later in the textbook that universal generalization is applied in every proof that uses the mathematical induction proof technique.

5.2.2. Rules of Inference for Existentially-Quantified Predicates

Existential instantiation states that, from the premise \(\exists x P(x),\) you can conclude that there must be at least one \(c \in U\) such that \(P(c)\) is true. This allows you to pick a "constant" \(c\) that makes the predicate \(P(x)\) True instead of needing to refer repeatedly to the existential quantifier.

Existential Instantiation (Existential Elimination)

  • \(\exists x P(x)\)

  • \(\therefore P(c) \text{ for some element } c \in U\)

Existential generalization states that, from the premise that \(P(c)\) is True for at least one \(c \in U,\) you can conclude that \(\exists x P(x)\) must also be True.

Existential Generalization

  • \(P(c) \text{ for some element } c \in U\)

  • \(\therefore \exists x P(x)\)

5.3. Proof Techniques

In this section several examples of formal mathematical proofs are given to illustrate different proof techniques. Many of the techniques correspond to certain rules of inference that were discussed earlier in this chapter.

Each proof starts by stating a conjecture, which is a proposition with undetermined truth value. The goal of each proof is to determine the truth value of the relevant conjecture.

To simplify the description of the proof techniques, we’ll only consider the case where the proof has a single premise \(p\), that is, we’ll always assume that our proof involves a single conditional \(p \rightarrow q\). This may seem like an oversimplification, but it is not: We are simply renaming the conjunction \((p_{1} \land p_{2} \land \ldots \land p_{n})\) of all of the actual premises by using the single propositional variable \(p\), that is we are defining \(p\) by the logical equivalence \(p \equiv (p_{1} \land p_{2} \land \ldots \land p_{n})\)

Here we’ll present examples of proofs using several different techniques. Most of these proofs establish an arithmetic fact that you probably have always known (or assumed) is True; instead, you can focus on the form of the proof: Note the steps that are used, and how the argument flows.

Another important proof technique, mathematical induction, will be discussed in a later chapter.

Example 3 - Why do we need proofs at all?

Consider the following proposition: "For all natural numbers \(n,\) the value of \(n^{2} + n + 41\) is a prime integer."

For each of the natural numbers 0, 1, …​, 10, the predicate \(P(n)\): "\(n^{2} + n + 41\) is a prime integer." evaluates to a proposition that is True. In fact, \(P(n)\) evaluates to a proposition that is True for each of the natural numbers \(n\) that is less than or equal to 40.

It may seem that we have "checked enough cases" to conclude that \(P(n)\) will evaluate to a proposition that is True for every possible natural number value of \(n.\) However, \(P(41)\) is the proposition "\(41^{2} + 41 + 41 \text{is a prime integer}\)," which is False - notice that \(41^{2} + 41 + 41 = 41 \cdot (41 + 1 + 1) = 41 \cdot 43\) is a composite number.

This example shows that it is not enough to verify that a proposition or predicate is True for just a few cases, unless those cases happen to cover every possibility.

5.3.1. Direct Proof

In a direct proof, we make an argument that a conditional statement \(p \rightarrow q\) must be True. This means that we can assume that the premise \(p\) is True and apply modus ponens to prove that \(q\) must be True, too.

Theorem

If \(a,\) \(b,\) and \(c\) are integers such that both \(a\) and \(b\) are divisible by \(c,\) then for any integers \(m\) and \(n\) the integer \(ma+nb\) must be divisible by \(c.\)
This statement can be rephrased as "If the integers \(a\) and \(b\) are multiples of the integer \(c\), then any sum of integer multiples of \(a\) and \(b\) must also be a multiple of \(c."\)

Proof

Before starting the formal proof, let’s look at a specific example. The integers 10, 6, and 2 are such that both 10 and 6 are divisible by 2. Suppose we have a pair of integers that we will use as multipliers, say 11 and 7, to form a new number \((11)(10)+(7)(6).\) Is the new number also divisible by 2? The answer is obviously "Yes" since we can just simplify the sum and divide by 2, but how can we justify this for every choice of the pair of multipliers? Notice that we can factor 2 out of 10 and 6 in the sum that defines our new number: \[ (11)(10) + (7)(6) = (11)(5)(2) + (7)(3)(2) = [(11)(5)+(7)(3)](2) \] We can find the common factor of 2 and "factor it out" as if it were a variable. This appears to work no matter what values are chosen for the first three integers and the pair of multipliers, so should be generalizable to a formal proof.

For the formal proof, start by supposing that \(a,\) \(b,\) and \(c\) are integers such that both \(a\) and \(b\) are divisible by \(c.\) This means that there are integers \(q\) and \(t\) such that \[ a=qc \text{ and } b=tc \]

For any integers \(m\) and \(n\), we can rewrite the expression \(ma+nb\) as \[ ma+nb = m(qc)+n(tc) = (mq)c + (nt)c = (mq+nt)c \]

The last part of the extended equality shows that \(ma+nb\) is a multiple of \(c,\) that is, \(ma+nb\) is divisible by \(c.\)

This shows that the statement of the theorem is a True proposition.

Q.E.D.

You Try

Write a proof of the following statement: If \(a,\) \(b,\) and \(c\) are integers such that \(a\) is divisible by \(b\) and \(b\) is divisible by \(c,\) then \(a\) must be divisible by \(c.\)

5.3.2. Proof By Contraposition

In a proof by contraposition, we make an argument that \(p \rightarrow q\) is True by instead first arguing that its contrapositive \(\neg q \rightarrow \neg p\) is True and secondly applying the logical equivalence of the conditional and its contrapositive. Start by assuming that the premise \(\neg q\) is True and apply modus ponens to prove that \(\neq p\) must be True, too, then apply logical equivalence.

Theorem

Let \(n\) represent an integer.

If \(n^{2}\) is even, then the integer \(n\) is even.

Proof

It is easier to prove "if it’s not the case that the integer \(n\) is even, then it’s not the case that \(n^{2}\) is even," so start by supposing that it’s not the case that the integer \(n\) is even.

This means that \(n\) must be odd, so there is an integer \(q\) such that \[ n = 2q + 1\]

This in turn means that \[ n^{2} = (2q + 1)^{2} = 4q^{2} + 4q + 1 = 2(2q^{2} + 2q) + 1\]

The last part of the extended equality shows that \(n^{2}\) is odd: When \(n^{2}\) is divided by 2, the remainder is 1. That is, \(n^2\) is not even.

This shows that the contrapositive of the statement of the theorem, "if the integer \(n\) is not even, then \(n^{2}\) is not even" is a True proposition. Since every conditional and its contrapositive are logically equivalent, this argument proves that "If \(n^{2}\) is even, then the integer \(n\) is even" is a True proposition.

Q.E.D.

You try

Prove the following statement: If \(n^{2}\) is odd, then the integer \(n\) is odd.

5.3.3. Proof By Counterexample

In a proof by counterexample, we disprove a proposition of the form \((\forall x \in D) P(x)\) by arguing that there is at least one value \(c \in D\) such that \(\neg P(c)\) is True.

Conjecture

For every natural number \(n,\) there are natural numbers \(a,\) \(b,\) and \(c\) such that \(n = a^{2} + b^{2} + c^{2}.\)

Disproof of Conjecture

In this case, we can simply compute values of the expression \(a^{2} + b^{2} + c^{2}\) until we find a "gap." \[ 0^{2} + 0^{2} + 0^{2} = 0 \] \[ 1^{2} + 0^{2} + 0^{2} = 1 \] \[ 1^{2} + 1^{2} + 0^{2} = 2 \] \[ 1^{2} + 1^{2} + 1^{2} = 3 \] \[ 2^{2} + 0^{2} + 0^{2} = 4 \] \[ 2^{2} + 1^{2} + 0^{2} = 5 \] \[ 2^{2} + 1^{2} + 1^{2} = 6 \] \[ 2^{2} + 2^{2} + 0^{2} = 8 \] \[ 2^{2} + 2^{2} + 1^{2} = 9 \] \[ 3^{2} + 0^{2} + 0^{2} = 9 \] Notice that you cannot write 7 as a sum of three squares of natural numbers (There may be other numbers that cannot be written in this form, too, but 7 is the least such number and we only need to find one counterexample.)

This proves the negation of the Claim, namely

Theorem

There exists at least one natural number \(n,\) such that for all natural numbers \(a,\) \(b,\) and \(c,\) \(n \neq a^{2} + b^{2} + c^{2}.\)

This may seem like a strange conjecture to consider until you find out that every natural number \(n\) can be written as \(n = a^{2} + b^{2} + c^{2} + d^{2}\) for some natural numbers \(a,\) \(b,\) \(c,\) and \(d,\) and that this may have been known about 1,800 years ago.

5.3.4. Proof by Contradiction

In a proof by contradiction, we disprove the proposition \(\neg p\) by making an argument that the conditional \(\neg p \rightarrow (q \land \neg q)\) must be True for some proposition \(q\) and apply the Contradiction Rule to conclude that \(p\) must be True.
Note: Sometimes, we argue instead that the proposition \(((\neg p \rightarrow q) \land (\neg p \rightarrow \neg q))\) must be True, and use the fact that this proposition is logically equivalent to \(\neg p \rightarrow (q \land \neg q)\) and apply the Contradiction Rule.

Theorem

There are no positive integers \(a\) and \(b\) such that \(\displaystyle{ \left( \frac{a}{b} \right)^{2} } = 2.\)

Proof

It may be helpful to write the proposition out in symbols: \[ \neg (\exists a \in \mathbb{Z}) (\exists b \in \mathbb{Z}) \left( a > 0 \land b>0 \land \left( \frac{a}{b} \right)^{2} = 2 \right) \]

To prove this proposition by contradiction, we ASSUME that its negation is True, that is we use the premise \[ \text{ Premise: } \neg \neg (\exists a \in \mathbb{Z}) (\exists b \in \mathbb{Z}) \left( a > 0 \land b>0 \land \left( \frac{a}{b} \right)^{2} = 2 \right) \] In words, we assume: There are integers \(a\) and \(b\) such that \(a > 0,\) \(b > 0,\) and \(\displaystyle{ \left( \frac{a}{b} \right)^{2} } = 2.\)

We know that we can reduce the fraction so that \(a\) and \(b\) have no common prime factors (You know how to do this - just divide both numerator and denominator by their greatest common divisor. In fact, we will prove that this can be done in the mathematical induction chapter later in the textbook, but for now just treat it like a "known fact".)

To eliminate the fraction we can rewrite the equation as \[ a^{2} = 2 b^{2} \]

From this new equation, \(a^{2}\) must be divisible by 2. Use the theorem we proved earlier in this section to conclude that \(a\) must be divisible by 2, too. This means that there is an integer \(q\) such that \(a = 2q.\) Substitute the last expression for \(a\) in the equation to get \[ (2q)^{2} = 2 b^{2} \] which we can rewrite as \[ 4 q^{2} = 2 b^{2} \] or \[ 2 q^{2} = b^{2} \] From this equation, \(b^{2}\) is divisible by 2, and we can conclude that \(b\) is divisible by 2, too.

So…​ we have positive integers \(a\) and \(b\) that have no common prime factors, and we have proven that \(a\) and \(b\) have a common prime factor, namely 2. We have arrived at a contradiction.

Apply the Contradiction Rule to infer that the premise must be False.

We have proven the following theorem.

Theorem

There are no positive integers \(a\) and \(b\) such that \(\displaystyle{ \left( \frac{a}{b} \right)^{2} } = 2.\)

That is, the square root of 2 is not a rational number.

Here is another example of proof by contradiction.

Theorem - Generalized Pigeonhole Principle

Suppose that \(n\) and \(k\) are positive integers. If each of \(n\) objects is assigned to one of \(k\) categories, then at least one category contains at least \(\displaystyle{\left\lceil \frac{n}{k} \right\rceil}\) objects.

Proof

First, recall that \(\lceil x \rceil\) is the ceiling function whose output is the least integer that is greater than or equal to \(x\) (that is, \(\lceil x \rceil\) rounds a real number \(x\) up to the next greatest integer.) The graph of the function is shown in section 3 of this appendix.

Next, before starting a formal proof, let’s look at a specific example to understand what we need to prove. Suppose we want to assign 13 people to the 3 categories "high school student," "post-secondary student," and "other". It’s not hard to see that when we assign people to the categories, the sum of the numbers in the categories has to be 13, so at least one of the categories has at least \(5 = \displaystyle{\left\lceil \frac{13}{3} \right\rceil}\) people. That is, if each category had at most \(4 = \displaystyle{\left\lceil \frac{13}{3} \right\rceil - 1}\) people, then the sum of those numbers would be at most \((3)(4) = 12,\) but we know that the sum should be equal to 13 - this is a contradiction. You can formalize this argument to use \(n\) and \(k\) instead of the specific values 13 and 3, which will provide a formal proof using the "proof by contradiction" technique.

Now, to prove this proposition by contradiction, suppose that the conditional is False. That is, we assume that

  • It is True that \(n\) and \(k\) are positive integers.

  • It is true that each of \(n\) objects has been assigned to one of \(k\) categories.

  • It is False that "At least one category contains at least \(\displaystyle{\left\lceil \frac{n}{k} \right\rceil}\) objects."

So we are assuming that the negation of the last bulleted statement must be True, that is "Every category contains fewer than \(\displaystyle{\left\lceil \frac{n}{k} \right\rceil}\) objects" is True. You should verify that this is the correct negation by using De Morgan’s laws for quantifiers.

Label the categories with the integers \(1, 2, \ldots k\) and let the integers \(c_1, c_2, \ldots, c_k\) be the counts of objects in each of the categories, that is, assume that the number of objects assigned to category \(i\) is \(c_i.\) From the assumption, every \(c_i\) is less than or equal to \(\displaystyle{\left\lceil \frac{n}{k} \right\rceil} - 1.\) The total number of objects assigned to categories is therefore \[ c_1 + c_2 + \cdots + c_k \leq k \left( \displaystyle{\left\lceil \frac{n}{k} \right\rceil} - 1 \right) \]

For any real number \(x,\) it is true by definition of the ceiling function that \(\displaystyle{x \leq \left\lceil x \right\rceil < x+1}\)

This means that \[ c_1 + c_2 + \cdots + c_k \leq k \left( \displaystyle{\left\lceil \frac{n}{k} \right\rceil} - 1 \right) < k \left( \displaystyle{\left( \frac{n}{k} + 1 \right)} - 1 \right) \] and the expression on the right simplifies to \(n.\)

So the number of objects assigned to the categories must be strictly less than \(n,\) but we also have as a premise that all \(n\) objects were assigned. This is a contradiction.

Apply the Contradiction Rule to infer that it is False that the last bulleted statement is False, that is, conclude that the conditional statement of the theorem must be True.

We have proven the theorem.

Theorem

Suppose that \(n\) and \(k\) are positive integers.

If each of \(n\) objects is assigned to one of \(k\) categories, then at least one category contains at least \(\displaystyle{\left\lceil \frac{n}{k} \right\rceil}\) objects.

5.3.5. Proof By Exhaustion (Proof By Cases)

Sometimes it is convenient to break a proof into a finite number of cases. For example, it may be easier to prove a statement that involves an integer by considering a first case where the integer is odd and a separate second case where the integer is even, then combining the two separate cases to create a single proof for all integers \(n.\)

In a general proof by cases, you make an argument that a conditional statement \((p_{1} \lor \cdots \lor p_{n}) \rightarrow r\) must be True. This means that if any one of the "cases" \(p_{i},\) where \(i \in \{ 1, 2, \ldots , n \},\) is True, you can apply the tautology \(p_{i} \rightarrow (p_{1} \lor \cdots \lor p_{n})\) and the transitivity rule of inference to prove that \(r\) must be True, too.

A proof by exhaustion is a special kind of proof by cases where the premise is of the form \((p_{1} \lor \cdots \lor p_{n} \lor \neg (p_{1} \lor \cdots \lor p_{n}) ).\) Notice that this premise must be True since if all of \(p_{1},\) \(p_{2},\)… \(p_{n}\) are False then \(\neg (p_{1} \lor \cdots \lor p_{n})\) is True.

If there are two cases, proof by exhaustion corresponds to using the "proof by cases" rule of inference discussed above in the section "Other Common Rules Of Inference." The tautology can be rewritten in the simpler form \(((p \rightarrow r) \land (\neg p \rightarrow r)) \rightarrow r\) because \(p \lor \neg p\) must always be True.

If there are more than two cases, this corresponds to using the tautology \(((p_{1} \rightarrow r) \land ... \land (p_{n} \rightarrow r) \land (\neg (p_{1} \lor \cdots \lor p_{n}) \rightarrow r)) \rightarrow r\).

Example 4 - Working with multiple cases

Let’s prove the following theorem: \[ \text{If \(n\) is an integer, then \(n(n+1)\) is an even integer.} \]

Proof

Consider the following two cases:

  • Case 1: \(n\) is an odd integer.
    In this case, \(n+1\) must be an even integer, and \(n(n+1)\) is the product of an odd integer and an even integer so must be even. (Note that this could be made more formal by stating that there is some integer \(j\) such that \(n+1 = 2j\) so that \(n(n+1) = n(2j) = (2j)n = 2(jn).\))

  • Case 2: \(n\) is an even integer.
    In this case, \(n+1\) must be an odd integer, and \(n(n+1)\) is the product of an even integer and an odd integer so must be even. (Note again that this could be made more formal by stating that there is some integer \(k\) such that \(n = 2k\) so that \(n(n+1) = (2k)(n+1) = 2((k)(n+1)).\))

Since the statement "\(n\) is an odd integer or \(n\) is an even integer" must be True no matter what value the integer \(n\) has, this shows that the statement of the theorem is a True proposition.

Q.E.D.