4. Logic
CAUTION - CHAPTER UNDER CONSTRUCTION!
NOTICE: If you are enrolled in the CSC 230 course that I teach at SFSU, you need to use the “CSC230 version” of the book, which I will be updating throughout the semester. The version you are looking at now is the “public version” of the book that will not be updated again before the start of June 2026.
This chapter was last updated on February 18, 2025.
Added link to DNF and CNF website
Contents locked until 11:59 p.m. Pacific Standard Time on May 23, 2025.
Logic is the study of reasoning. Logic is used to create, analyze, and validate arguments, where an argument is a finite sequence of statements that ends with a conclusion based on inferences made from earlier statements in the argument.
Among the applications of logic to computer science are design of electronic circuits and validation of algorithms and programs.
Key terms and concepts covered in this chapter:
-
Propositional logic (also called "propositional calculus")
-
Logical operators (also called "logical connectives")
-
Negation ("not")
-
Conjunction ("and")
-
Disjunction ("or")
-
Conditional ("implication")
-
The converse, inverse, and contrapositive of a conditional
-
-
Biconditional ("if and only if," abbreviated as "iff")
-
-
Truth tables
-
Well-formed formulas
-
Satisfiability, tautology, and contradiction
-
Normal forms (conjunctive and disjunctive)
-
-
Predicate logic
-
Predicates as "statement-valued functions"
-
Quantification of Predicates
-
Universal quantifier
-
Existential quantifier
-
-
-
To be added to this chapter after May 23, 2025:
-
Limitations of propositional and predicate logic (e.g., expressiveness issues)
-
Boolean algebra and Boolean circuits
-
4.1. Propositional Logic
A proposition is a statement that declares a fact that is either True or False (but not both!)
Propositional logic consists of a set of formal rules for combining propositions in order to derive new propositions.
A goal of propositional logic is to have a method for creating valid arguments that are sequences of propositions, where the correctness and validity of the argument is based solely on the propositions' truth values (True and False), ignoring the actual content of the propositions. Compare this to doing algebra: You can write \(2 (x + 3 y) = 2x + 6y\) because it is a correct and valid step to distribute multiplication over addition. You can do the algebra and ignore the specific numerical values (the "numerical content") that \(x\) and \(y\) stand for.
In propositional logic, it is traditional to use propositional variables such as p, q, and r to stand for the possible assignments of truth values to propositions; often, the propositional variables themselves are referred to as the propositions. Again, compare this to the algebraic example where you can treat \(x\) and \(y\) as numbers even though they are actually variables that stand for numbers.
What is the advantage of using symbols? A long time ago, philosophers discovered that is easier to follow lines of reasoning by putting our thoughts into symbols. This was an important step in the eventual development of modern technological society and, in particular, electronic computers. Before a computer can do its work, humans need to put our thoughts into them; however, a spoken language like English can be too difficult to use because many different phrases can represent the same logical statements.
You can build compound propositions (also called "propositional functions") from simpler propositions. For example, in the preceding example, the compound propostion "if p then q " was introduced as a new proposition built from the propositional variables p and q . In the next section, you will learn how to represent compound propositions using symbols.
4.2. Logical Operations and Truth Tables
In this section, compound propostions will be represented by using propositional variables and logical operator symbols (also called "logical operations" or "logical connectives") Once again, you can compare this to how numerical and algebraic relationships can be represented in symbols using algebraic expressions built with the usual arithmetic operator symbols with variables and numerals.
|
In Python, we use \(\texttt{Boolean}\) variables to represent propositions and define functions for each compound proposition. Each compound proposition can implemented using the \(\texttt{Boolean}\) operations \(\texttt{not}\), \(\texttt{and}\), and \(\texttt{or}\) discussed in the section Operators and Expressions in the chapter "Appendix: An Introduction to Python". |
A truth table can be used to display the truth values of a compound proposition that is built from propositional variables and logical operators. A truth table is created with rows representing all possible interpretations of the propositional variables, that is, all possible assignments of truth values to the propositional variables. Each column of a truth table displays the truth values for either one of the propositional variables or a compound proposition built up from propositional variables and/or simpler compound propositions. As an analogy, think of how a table can be used to display the numerical input and output values of a function represented by an algebraic expression.
The most commonly-used logical operators are described in the rest of this section.
4.2.1. Negation
"I am not an astronaut."
The
negation
of a proposition \(p\), denoted in mathematics by \(\neg p\) and
read as "not \(p\)", is the proposition
"It is
not the case
that \(p\)".
The proposition \(\neg p\) has the opposite truth value to \(p.\)
Other textbooks and sources may use \(\overline{p}\) or \(\sim \! p\) to represent \(\neg p.\)
| \(p\) | \(\neg p\) |
|---|---|
|
True |
False |
|
False |
True |
For example, the negation of the proposition "Today is Friday." would be
"It is not the case that today is Friday." or more succinctly "Today is not Friday."
For a proposition \(p,\) exactly one of \(p\) and \(\neg p\) is True and exactly one is False. Two propositions can be contrary (that is, they could not both be True) without being negations of each other: As an example, both of the propositions "Today is Friday." and "Today is Saturday." could be False, so "Today is Saturday." is not the negation of "Today is Friday."
Notice that the two propositions \(p\) and \(\neg (\neg p)\) must always have the same truth value (You can see this by inserting a column for \(\neg (\neg p)\) in the truth table shown earlier in this subsection.)
| In the first few truth tables in this chapter, "True" and "False" are spelled out, but it is more often the case that these words are abbreviated to their first letters, "T" and "F" in truth tables. |
4.2.2. Conjunction
"I am a rock and I am an island."
Let \(p\) and \(q\) be propositions. The conjunction of \(p\) and \(q\), denoted in mathematics by \(p \land q\) and read as "\(p\) and \(q\)", is True when both \(p\) and \(q\) are True and is False otherwise.
| \(p\) | \(q\) | \(p \land q\) |
|---|---|---|
|
True |
True |
True |
|
True |
False |
False |
|
False |
True |
False |
|
False |
False |
False |
Notice that the two propositions \(p \land q\) and \(q \land p\) always have the same truth value.
4.2.3. Disjunction
"They studied hard or they are extremely bright."
Let \(p\) and \(q\) be propositions. The disjunction of \(p\) and \(q\), denoted in mathematics by \(p \lor q\) and read as "\(p\) or \(q\)", is True when at least one of \(p\) and \(q\) are True and is False otherwise.
| \(p\) | \(q\) | \(p \lor q\) |
|---|---|---|
|
True |
True |
True |
|
True |
False |
True |
|
False |
True |
True |
|
False |
False |
False |
Notice that the two propositions \(p \lor q\) and \(q \lor p\) always have the same truth value.
4.2.4. Conditional
" If you get a 100 on the final exam, then you earn an A in the class."
Let \(p\) and \(q\) be propositions. The
conditional statement
\(p \rightarrow q\), read as "if
p
then
q
", "
p
implies
q
", or, more formally, "the conditional with hypothesis
p
and conclusion
q
", is the proposition that is False when
p
is True and
q
is False, and True otherwise. The conditional statement \(p \rightarrow q\) is also called "the implication \(p \rightarrow q\)".
The conditional \(p \rightarrow q\) can also be denoted by \(p \Rightarrow q\) or \(p \implies q.\) In addition, there are many other ways to express the conditional \(p \rightarrow q\) in English, two of which are "
p
only if
q
" and "
q
if
p
".
| \(p\) | \(q\) | \(p \rightarrow q\) |
|---|---|---|
|
True |
True |
True |
|
True |
False |
False |
|
False |
True |
True |
|
False |
False |
True |
|
|
The Converse, Contrapositive and Inverse of a Conditional Statement
Given propositions p and q , we can form three additional compound propositions that are related to the conditional \(p \rightarrow q\):
-
\(q \rightarrow p\), called the converse of \(p \rightarrow q\)
-
\( \neg q \rightarrow \neg p\), called the contrapositive of \(p \rightarrow q\)
-
\( \neg p \rightarrow \neg q\), called the inverse of \(p \rightarrow q\)
The extended truth table for the conditional and the three related propositions is shown below.
| \(p\) | \(q\) | \(p \rightarrow q\) (conditional) | \(q \rightarrow p \) (converse) | \( \neg q \rightarrow \neg p\) (contrapositive) | \( \neg p \rightarrow \neg q\) (inverse) |
|---|---|---|---|---|---|
|
True |
True |
True |
True |
True |
True |
|
True |
False |
False |
True |
False |
True |
|
False |
True |
True |
False |
True |
False |
|
False |
False |
True |
True |
True |
True |
|
From the truth table it can be seen that
|
In the section on logically equivalent propositions we will discuss the bullet points in the preceding note in more detail.
The next example illustrates these four propositions.
4.2.5. Biconditional
"It is raining outside if and only if it is a cloudy day."
Let \(p\) and \(q\) be propositions. The biconditional \(p \leftrightarrow q\), read as " p if and only if q ", is the proposition that is True when p and q have the same truth value, and False otherwise. The biconditional is also called "the bi-implication". Note that \(p \leftrightarrow q\) can also be denoted by \(p \Leftrightarrow q\) or \(p \iff q.\)
| \(p\) | \(q\) | \(p \leftrightarrow q\) |
|---|---|---|
|
True |
True |
True |
|
True |
False |
False |
|
False |
True |
False |
|
False |
False |
True |
You can use a truth table to show that two propositions \(p \leftrightarrow q\) and \(q \leftrightarrow p\) always have the same truth value.
|
The biconditional \(p \leftrightarrow q\) is read as " p if and only if q " because it has the same truth table as the conjunction of the two conditionals " p if q " (that is, \(q \rightarrow p\)) and " p only if q " (that is, \(p \rightarrow q\)). |
It is important to contrast the conditional with the biconditional. Consider the conditional example "If you get a 100 on the final exam, then you earn an A in the class." This means that when you get a 100 on the final you also get an A in the class. The conditional represents a one-way contract: You earn an A in the class if you get a 100 on the final exam. There is nothing said about the result (the grade you earn in the class) if you do NOT meet the condition (get a 100 on the final exam).
As a biconditional the example would say "You get a 100 on the final exam if and only if you earn an A in the class." This becomes a two-way contract: You earn an A in the class if you get a 100 on the final, but you do not earn an A in the class if you do not get a 100 on the final.
4.2.6. Other Compound Propositions
The negation, disjunction, conjunction, conditional, and biconditional are the most commonly-used logical operators for forming compound propostions and will be the ones used throughout the rest of this chapter. However, there are at least three others you should know about.
Exclusive Disjunction
"I took either 2 Advil or 2 Tylenol."
Let \(p\) and \(q\) be propositions. The exclusive disjunction of \(p\) and \(q\) (also known as xor ), denoted in mathematics by \(p \oplus q\), is True when exactly one of \(p\) and \(q\) are True and False otherwise.
| \(p\) | \(q\) | \(p \oplus q\) |
|---|---|---|
|
True |
True |
False |
|
True |
False |
True |
|
False |
True |
True |
|
False |
False |
False |
Notice that the two propositions \(p \oplus q\) and \(q \oplus p\) always have the same truth value.
The NAND and NOR Operators
The NAND and NOR operators correspond to two important digital logic gates used in electronic devices.
NAND
"An onion is not both a fruit and a vegetable."
Let \(p\) and \(q\) be propositions. In this textbook, the NAND of \(p\) and \(q\) is denoted by \(p \uparrow q\) and is False when both \(p\) and \(q\) are True and is True otherwise. That is, the NAND is the negation of \(p \land q\) - think of NAND as "Not AND."
| \(p\) | \(q\) | \(p \uparrow q\) |
|---|---|---|
|
True |
True |
False |
|
True |
False |
True |
|
False |
True |
True |
|
False |
False |
True |
Notice that the two propositions \(p \uparrow q\) and \(q \uparrow p\) always have the same truth value.
NOR
"This pen’s ink is neither red nor blue."
Let \(p\) and \(q\) be propositions. In this textbook, the NOR of \(p\) and \(q\) is denoted by \(p \downarrow q\) and is True when both of \(p\) and \(q\) are False and is False otherwise. The NOR is also referred to as "joint denial" since it is True exactly when neither \(p\) nor \(q\) is True. That is, the NOR is the negation of \(p \lor q.\)
| \(p\) | \(q\) | \(p \downarrow q\) |
|---|---|---|
|
True |
True |
False |
|
True |
False |
False |
|
False |
True |
False |
|
False |
False |
True |
Notice that the two propositions \(p \downarrow q\) and \(q \downarrow p\) always have the same truth value.
4.2.7. Well-Formed Formulae and Operator Precedence (Order Of Operations)
A well-formed formula (or wff for short) is a string of symbols that represents a compound propsition.
Here is a recursive definition of wff:
-
A propositional variable is a well-formed formula.
-
If \(\alpha\) ("alpha") and \(\beta\) ("beta") are well-formed formulas, then the following are also well-formed formulas:
-
\(\left( \neg \alpha \right)\)
-
\(\left( \alpha \land \beta \right)\)
-
\(\left( \alpha \lor \beta \right)\)
-
\(\left( \alpha \rightarrow \beta \right)\)
-
\(\left( \alpha \leftrightarrow \beta \right)\)
-
The definition of wff allows you or, even better, a computer to analyze any string of symbols to determine whether the string of symbols is a wff. For example, \((p \land q \lor r)\) isn’t a wff but both \((p \land (q \lor r))\) and \(((p \land q) \lor r)\) are wffs. You could write code to implement an algorithm to validate a string as a wff.
It can be shown that every compound proposition can be represented by at least one wff. However, a wff may be difficult to read quickly if it contains many parentheses. As an example, it is not easy to read \(( (p \rightarrow q) \lor ( (\neg r) \land (s \leftrightarrow t) ) )\). For this reason, we can introduce operator precedence rules that allow us to eliminate some of the parentheses.
To evaluate a compound proposition, we start by evaluating
-
all expressions enclosed in parentheses from left to right, then
-
all negations from left to right, then
-
all conjunctions from left to right, then
-
all disjunctions from left to right, then
-
all conditionals from left to right, and finally
-
all biconditionals from left to right.
This allows us to drop some parentheses from a wff that represents a compound proposition.
For example, the compound proposition \(\neg p \lor q \land r \rightarrow s\) represents the same proposition as the wff \((((\neg p) \lor (q \land r)) \rightarrow s)\). At least some of the parentheses must be used if you want to represent a different proposition such as \((\neg p \lor q) \land (r \rightarrow s)\).
4.2.8. Truth Tables of Compound Propositions
To compute the truth values of a longer compound proposition or wff by hand, it can be useful to break up the proposition or wff into the smaller propositions or wffs that it was built from.
When creating your own truth table it is crucial to be systematic about ensuring you have all possible truth values for each of the simple propositions. Each simple proposition has two possible truth values, so the number of rows in the table should be \(2^n\) where \(n\) is the number of propositions (Do you recall why the number of rows must be \(2^n\)?) You should also consider breaking complex propositions into smaller pieces.
4.3. Logically Equivalent Propositions
Recall that an interpretation of a proposition is an assignment of truth values to the propositional variables.
Two propositions are considered logically equivalent (or simply equivalent ) if they have the same truth values for every possible interpretation. It is often easiest to see this by constructing a truth table for the two propositions and comparing.
We use the symbol \(\equiv\) to denote that two propositions are logically equivalent. So in the preceding example, we would write \(\neg p \lor q \equiv p\rightarrow q\).
| \(\equiv\) is NOT a logical operator used to build compound propositions, but instead is used to say that two propositions are logically equivalent. This is similar to how \(=\) is used in arithmetic: We can write \(2 + 2 = 5 - 1\) to say that \(2 + 2\) and \(5 - 1\) are numerically equivalent, but we don’t use the \(=\) sign as an arithmetic operator to actually do any arithmetic. |
| Saying that two propositions p and q are logically equivalent is the same as saying that the biconditional compound proposition \(p \leftrightarrow q\) is always True. |
4.3.1. Tautologies, Contradictions and Contingencies
A proposition is a tautology if its truth value is always True. That is, a tautology is True for every possible interpretation of its propositional variables.
A proposition is called satisfiable if there is at least one interpretation for which the proposition is True.
A proposition is unsatisfiable if there is no interpretation for which the proposition is True.
A proposition is a contradiction if its truth value is always False. That is, a contradiction is False for every possible interpretation of its propositional variables. This is just another way of saying that it is unsatisfiable.
A proposition that is neither a tautology nor a contradiction is said to be a contingency since its truth value can be either True or False, contingent on the truth value assigned to its propositional variables.
The two compound propositions in the previous example are so important that they have their own names,
4.3.2. De Morgan’s Laws
Two important logical equivalences are De Morgan’s Law. These describe how to "distribute" the \(\neg\) operator across the \(\land\) and \(\lor\) operators.
De Morgan’s Laws can be verified by creating truth tables for \(\neg (p \land q) \leftrightarrow \neg p \lor \neg q\) and \(\neg (p \lor q) \leftrightarrow \neg p \land \neg q\) to show that these propositions are True for every interpretation of \(p\) and \(q\).
4.3.3. Some Other Logical Equivalencies
Here is a collection of additional equivalencies of compound propositions. Each of these can be verified by constructing a truth table to show that the biconditional of the left-hand side and the right-hand side of the logical equivalence is true for all interpretations of the propositional variables.
Double Negation: \[ p \equiv \neg (\neg p) \]
Commutative laws: \[ p \lor q \equiv q \lor p \] \[ p \land q \equiv q \land p \]
Associative laws: \[ p \lor (q \lor r) \equiv (p \lor q) \lor r \] \[ p \land (q \land r) \equiv (p \land q) \land r \]
Distributive laws: \[ p \lor (q \land r) \equiv (p \lor q) \land (p \lor r) \] \[ p \land (q \lor r) \equiv (p \land q) \lor (p \land r) \]
4.3.4. Disjunctive Normal Form (DNF)
It is traditional to focus on negation \(\neg\), conjunction \(\land\), and disjunction \(\lor\) as the three primary logical operations. This is because any compound proposition can be rewritten in terms of these three operations and the propositional variables present in the original compound proposition.
One way to justify this is by using an expression in disjunctive normal form (DNF), which is a disjunction of one or more conjunctions, where only one of the conjunctions can be true for any interpretation of the propositional variables. This description should become clearer after reading the following example.
4.3.5. Conjunctive Normal Form (CNF)
In some applications of propositional logic, it is more useful to find a logically equivalent expression for a given proposition that is written as a conjunction of several disjunctions. This conjunctive normal form (CNF) can be constructed as shown in the following example.
Here is a website that allows you to build the DNF and CNF for a given propositional function.
4.3.6. Functional Completeness
A set \(S\) of logical operators is called functionally complete if every compound proposition is logically equivalent to a compound proposition involving only operators that are members of \(S.\)
The importance of the NAND and NOR in electronic circuits arises from the following theorem.
4.4. Predicates and Quantifiers
Up to this point, most of our propositions have been of the form "Sarah earned a B.S. in Computer Science" - the proposition describes a single individual constant (in this case, "Sarah.")
However, we often need to discuss an entire category of individuals at once, which is equivalent to replacing the constant "Sarah" by a variable. We will discuss this idea in this section.
4.4.1. Predicates
A predicate is a statement that includes one or more variables such that when values are assigned to the variables the predicate becomes a proposition.
Predicates are denoted as \(P(x)\) or \(Q(x,y)\) where \(P\) and \(Q\) represent the statements and \(x\) and \(y\) are variables. After a value is assigned to each variable, the predicate becomes a proposition which has a truth value. That is, we "evaluate" a predicate by substituting inputs into the variables and get a proposition as the output.
4.4.2. Quantifiers
Consider the statements
-
For all integers \(x\), \(x^2\geq 0\).
-
Some student in the class has a birthday in July.
Each of these statements considers a proposition over an entire population or set, called the
domain,
and
describes whether at least one element, or all of the elements
in the
domain
satisfy the proposition.
There are two
commonly-used
quantifiers, the
universal quantifier
and the
existential quantifier
.
The domain is also called the
domain of discourse
or the
universe of discourse.
The Universal Quantifier, \(\forall,\) represents the statement "for all", "for every", "for each". When it comes before a statement, it means that statement is true for all values in the domain.
The Existential Quantifier, \(\exists,\) represents the statement "there exists", "for some", "at least one". When it comes before a statement, it means the statement is true for at least one value in the domain.
Recall the previous example statements:
-
For all integers \(x\), \(x^2 \geq 0\).
Let \(P(x)\) be the predicate "\(x^2 \geq 0\)". Then we write the statement as \(\forall x P(x)\), where the domain is the set of all integers. This quantified statement will be true since anytime you square a nonzero integer it is positive and \(0^2=0\).
-
Some student in the class has a birthday in July.
Let \(Q(s)\) be the predicate "student \(s\) has a birthday in July". Then we write the statement as \(\exists s Q(s)\), where the domain is the set of all students in the class. This statement will be true as long as at least one student in the class has a birthday in July. It will be false, otherwise.
4.4.3. Negation of Quantifiers
It is important to consider the negation of a quantified expression.
-
"Every student in this class has taken Programming Fundamentals."
This is a universally quantified statement and can be expressed as \(\forall x P(x)\) where \(P(x)\) is the statement "\(x\) has taken Programming Fundamentals" and the domain consists of all the students in this class. The negation of the statement would be "It is not true that every student in this has taken Programming Fundamentals." Equivalently,
-
"There is a student in this class who has NOT taken Programming Fundamentals."
This is an existentially quantified statement expressed as \(\exists x \neg P(x)\).
This demonstrates that the negation of a universally quantified statement is an existential statement. In symbols, we have \(\neg \forall x P(x)\equiv \exists x \neg P(x)\).
Similarly, the negation of an existential statement is a universal statement. \(\neg \exists x P(x) \equiv \forall x \neg P(x)\).
The predicate of a quantified statement could be a compound statement. For instance,
-
Some dogs are big and fluffy.
This is written as \(\exists x (B(x) \land F(x))\) where \(B(x)\) is the proposition "\(x\) is big." and \(F(x)\) is the proposition "\(x\) is fluffy." and the domain is dogs. Negating this statement would give
\(\neg \exists x (B(x) \land F(x)) \equiv \forall x \neg (B(x) \land F(x)) \equiv \forall x (\neg B(x) \lor \neg F(x))\)
In words,
-
All dogs are not big or not fluffy.
4.4.4. Nested Quantifiers
There are times it will take more than one quantifier to express a statement.
-
For all integers \(x\), there exists an integer \(y\), such that \(x+y=0\).
This statement contains both a universal and an existential quantifier. \(\forall x \exists y S(x,y)\) where \(x\) and \(y\) are integers and \(S(x,y)\) is the proposition \(x+y=0\). This statement means, if you have any integer \(x\) (for instance \(x=5\)) then you can find an integer \(y\) (for instance \(y=-5\)) such that \(x+y=0\).
The order of the quantifiers matters. \(\exists x \forall y S(x,y)\) would be
-
There exists an integer \(x\), such that for all integers \(y\), \(x+y=0\).
Note that in this statement you find an integer \(x\) so that when you add any integer \(y\) to it you always get 0.
The first statement, for all integers \(x\), there exists an integer \(y\) such that \(x+y=0\), is true. For any integer \(x\) you could choose \(y=-x\) and \(x+y=x+(-x)=0\). While the second statement, there exists an integer \(x\), such that for all integers \(y\), \(x+y=0\), is false.
To negate nested quantifiers, repeatedly apply De Morgan’s Laws of negating a quantifier and a predicate.
Namely, \(\neg \forall x P(x) \equiv \exists x \neg P(x)\) and \(\neg \exists x P(x) \equiv \forall x \neg P(x)\).
4.5. Applications of Logic
Remixer’s Note: This section is taken from the original “Discrete Math” book with minor edits to include base-two notation and a link to the NANDgame website.
In this section we consider two applications of logic to information technology and computer science. The first involves bitwise operations, and the second designing and analyzing logic circuits.
4.5.1. Bitwise operations
A bitwise operation is a Boolean operation that operates on the individual bits (\(0s\), or \(1s\)) of the operand(s) and are summarized
We summarize the truth tables for the bitwise boolean operators.
| \(p\) | \(q\) | \(AND\) & | \( \ OR\ | \) | \(XOR\) \({}^{\wedge}\) | \(IF\) \(\Rightarrow\) | \(IFF\) \(\Leftrightarrow\) |
|---|---|---|---|---|---|---|
|
1 |
1 |
1 |
1 |
0 |
1 |
1 |
|
1 |
0 |
0 |
1 |
1 |
0 |
0 |
|
0 |
1 |
0 |
1 |
1 |
1 |
0 |
|
0 |
0 |
0 |
0 |
0 |
1 |
1 |
4.5.2. Logic Circuits
Logic circuits are important in designing the arithmetic and logic units of a computer processor.
Consider the problem of adding two \(8\)-bit numbers in binary.
In binary, \((0)_2 + (0)_2 = (0)_2\) and \((0)_2 + (1)_2 = (1)_2 + (0)_2 = (1)_2\), but as in decimal addition, \((1)_2 + (1)_2 = (10)_2\) requires a carry, that is, the "sum bit" is \(0\) with a "carry bit" of \(1\) to the next significant column on the left.
Note: The bits are enclosed in parentheses which are followed by the subscript \(_2\) to emphasize that binary notation, not decimal notation, is being used. This notation is covered in much more detail in the
Number Bases
chapter.
Thinking then of adding a specific column of two binary digits, say \(A\) and \(B\), involves as input the bits \(A, B\) and the carry in from the previous column say \(C_{in}\). The output will be the sum \(S\) and the carry out to the next column, say \(C_{out}\). These are the basic components of what is called a binary adder.
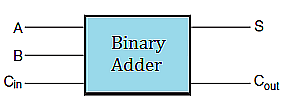
The logic table for binary addition based on the digital inputs \(A, B, C_{in}\), and digital outputs \(S\) and \(C_{out}\) is summarized in the table.
| \(A\) | \(B\) | \(C_{in}\) | \(\mathbf{S}\) | \(\mathbf{C_{out}}\) |
|---|---|---|---|---|
|
1 |
1 |
1 |
\(\mathbf{1}\) |
\(\mathbf{1}\) |
|
1 |
1 |
0 |
\(\mathbf{0}\) |
\(\mathbf{1}\) |
|
1 |
0 |
1 |
\(\mathbf{0}\) |
\(\mathbf{1}\) |
|
1 |
0 |
0 |
\(\mathbf{1}\) |
\(\mathbf{0}\) |
|
0 |
1 |
1 |
\(\mathbf{0}\) |
\(\mathbf{1}\) |
|
0 |
1 |
0 |
\(\mathbf{1}\) |
\(\mathbf{0}\) |
|
0 |
0 |
1 |
\(\mathbf{1}\) |
\(\mathbf{0}\) |
|
0 |
0 |
0 |
\(\mathbf{0}\) |
\(\mathbf{0}\) |
It can be shown that the logic for the outputs \(S\), and \(C_{out}\) is given by the following propositions \[ C_{out}=(A\land B)\lor \left(B\land C_{in}\right)\lor \left(A\land C_{in}\right)\] \[S=\left(\sim A\land \sim B\land C_{in}\right)\lor \left(\sim A\land B\land \sim C_{in}\right)\lor \left(A\land \sim B\land \sim C_{in}\right)\lor \left(A\land B\land C_{in}\right) \]
Implementing these logical outputs based on the inputs \((A,B, C_{in})\), is through the use of electronic circuits called logic gates.
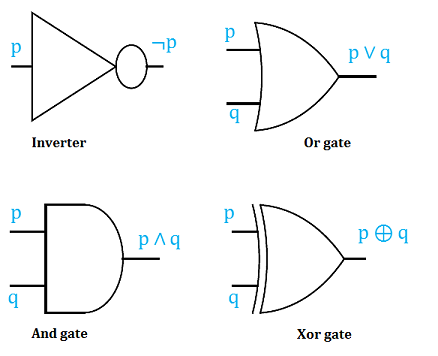
The basic logic gates, are the Inverter or Not gate, the And gate, the Or gate and the Xor gate. The graphical representation for each is shown below.
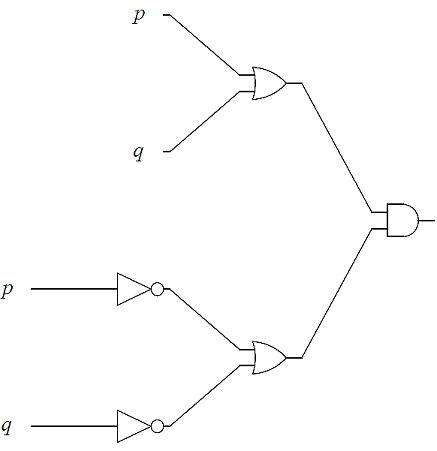
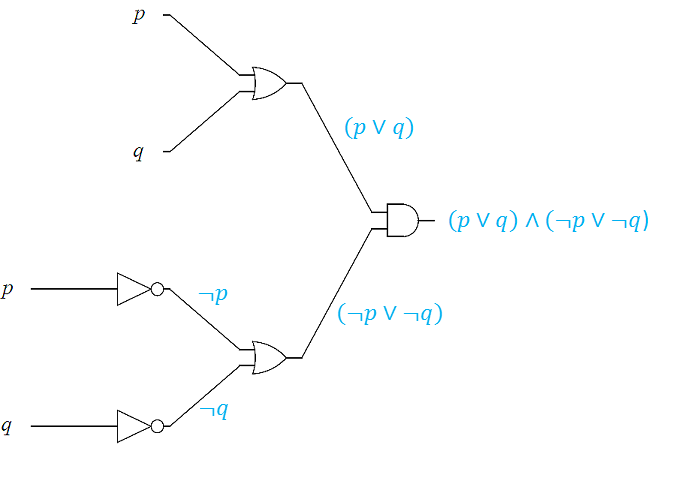
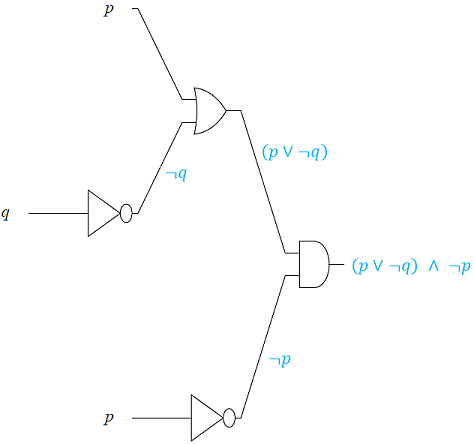
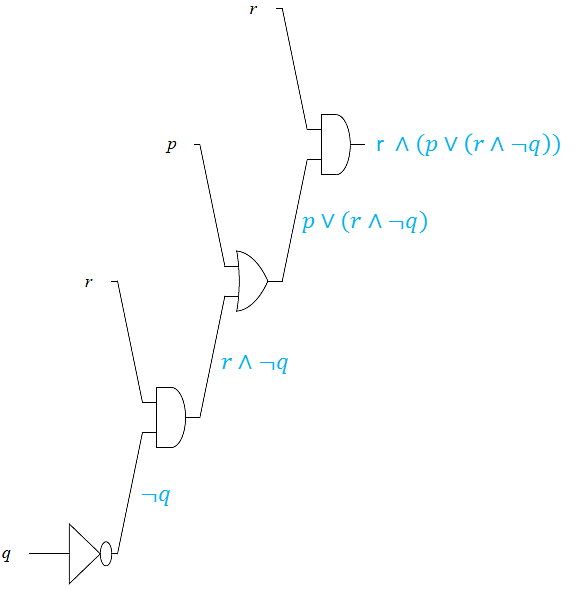
We end this section by first analyzing logic circuits to give their outputs in terms of their input variables, and then, constructing logic circuits based on logical statements.
In the next two examples, we design logic circuits based on logical propositions. The idea is to work backward using order of operations from the right to the left.
4.6. Exercises
Remixer’s Note: This section is taken from the original “Discrete Math” book with no changes.
-
Which of these statements are propositions? Explain your reasoning
-
Is Atlanta the capital of Georgia?
-
All birds fly
-
\(2\ \times\ \ 3\ =\ 5\)
-
\(5\ +\ 7\ =\ 7+5\)
-
\(x\ +\ 2\ =\ 11\)
-
Answer this question.
-
The rain in Spain
-
-
Construct truth tables for,
-
\(a\vee b\Rightarrow\lnot b\)
-
\((a\vee\lnot b)\ \Leftrightarrow\ a\)
-
\((a\Rightarrow b)\ \bigwedge\ (b\ \bigwedge\ \lnot c)\)
-
\((a\ \bigvee\ b)\ \Rightarrow\ (\ \lnot c\ \bigvee\ a)\)
-
\((a\ \bigvee\ b)\ \bigwedge\ (c\ \bigvee\lnot d\ )\)
-
\((\lnot c\ \bigwedge\ \ b)\ \bigvee\ \ (a\Rightarrow\ \lnot d\ )\)
-
-
Using truth tables, determine if each of the following is a tautology, contradiction, or neither (conditional)
-
\(\neg ((a\lor b)\lor (\neg a\land \neg b))\)
-
\(\left(\left(a\vee b\right)\land\lnot a\right)\Rightarrow b\)
-
\(\left(\left(a\vee b\right)\land a\right)\Rightarrow b\)
-
\(p\land r)\lor (\neg p\land \neg r)\)
-
\(\neg ((p\lor q)\lor (\neg p\land (\neg q\lor r)))\)
-
\(\neg (p\land q)\lor (q\lor r)\)
-
-
Using truth tables determine which of the following are equivalent
-
\(\left(p\Rightarrow q\right)\Rightarrow r\),
\(\left(p\land\lnot q\right)\vee r,\) and
\(\left(p\land\lnot q\right)\land r\)
-
\((a\lor b)\land c,\)
\((c\land a)\lor (c\land b),\) and
\(\neg ((\neg a\land \neg b)\lor \neg c)\)
-
-
Let \(C(x)\) be the statement "\(x\) has visited Canada." where the domain consists of the students at GGC. Express each of the quantifications in English.
-
\(\exists x C(x)\)
-
\(\forall x C(x)\)
-
How would you determine whether each of these statements is true or false?
-
-
Determine the truth value of each of these statements if the domain for all variables, \(m , n\) is the set of all integers, \(\mathbb{Z}\), explaining your reasoning.
-
\(\forall n:\left(n^2\geq 1\right)\)
-
\(\forall n:\left(n^2\geq 0\right)\)
-
\(\ \exists\ n:(n^2=3)\)
-
\(\ \exists\ m\forall\ n:(m+n=n-m)\)
-
\(\forall\ n\exists\ m:\ (n\cdot\ m=m)\)
-
\(\ \exists\ n\forall\ m:\ (n\cdot\ m=m)\)
-
\(\ \exists\ n\forall\ m:\ (n\cdot\ m=n)\)
-
-
Consider each of the compound propositions. (i) Translate each using logical symbols and letters, stating what each letter represents, (ii) Negate each using plain English sentences, and (iii) Translate the negated statements using logical symbols and quantifiers.
-
If it snows today, then I will go skiing tomorrow.
-
Mei walks or takes the bus to class.
-
Every person in this class understands mathematical induction.
-
In every mathematics class there is some student who falls asleep during lectures.
-
There is a building on the campus of some college in the United states in which every room is painted white.
-
-
Let \(p\), be the proposition ”My bicycle needs a tire replaced,” \(q\), be the proposition ”I will go cycling”, and, \(r\), be the proposition ”Rain is in the forecast.”
-
Express each of these compound propositions using plain English sentences.
-
\(\neg p\vee q\)
-
\(\neg p\Rightarrow \neg q\)
-
\((\neg p\wedge r)\Rightarrow q\)
-
\((\neg p\wedge r)\Rightarrow q\)
-
\((\neg p\wedge q)\vee r\)
-
-
Write these compound propositions using \(p\), \(q\) and, \(r\) and logical connectives (including negation).
-
If my bicycle tire does not replacement I will go cycling.
-
My bicycle tire does not replacement, there is rain in the forecast but I will go cycling
-
Whenever there is rain in the forecast, I do not go cycling.
-
If there is rain in the forecast or my tire needs replacement I will not go cycling.
-
Rain is not forecast whenever I go cycling.
-
Rain is not forecast and my tire does not need replacement whenever I go cycling.
-
-
-
Design logic circuits with the following output
-
\((p\lor (q\land \neg r))\lor \neg (p\land q)\)
-
\((p\lor (q\land r))\land \neg (p\land q)\)
-
-
Consider the predicate \(Q(x,y): x\ \cdot\ y=5\), where the domain of \(x\) and \(y\) is all positive real numbers \(\mathbb{R}^+\), or \(x,\ y\ >0\). Determine the true value of the following, an explain your reasoning.
-
\(Q(1,5)\)
-
\(Q\left(2,\frac{5}{2}\right)\)
-
\(\exists\ y,\ Q\left(7,y\right)\)
-
\(\ \forall\ y,\ Q\left(7,y\right)\)
-
\(\exists\ x\ \forall\ y,\ Q\left(x,y\right)\)
-
\(\ \forall\ \ x\ \exists\ \ y,\ Q\left(x,y\right)\)
-
-
Consider the predicate \(R(x,y):\ 2x+y=0\), where the domain of \(x\) and \(y\) is all rational numbers, \(\mathbb{Q}\). Determine the true value of the following, an explain your reasoning.
-
\(R(0,0)\)
-
\(R(2,-1)\)
-
\(R\left(\frac{1}{5},-\frac{2}{5}\right)\)
-
\(\exists y,\ R\left(0.2,y\right)\)
-
\(\ \forall y,\ R\left(7,y\right)\)
-
\(\exists\ x\forall\ y,\ R\left(x,y\right)\)
-
\(\ \forall\ x\ \exists\ y,\ R\left(x,y\right)\)
-
-
Calculate the bitwise \(AND\), the bitwise \(OR\), and the bitwise \(XOR\) of the following pairs of bytes, or sequence of bytes
-
\(01111111\) and \(11101001\)
-
\(1110010111111010\) and \(0101110101100011\)
-
-
Give the output for each of the logic circuits in terms of the input variables,
-
The logic circuit, with input variables, \(p, q\), \(r\).
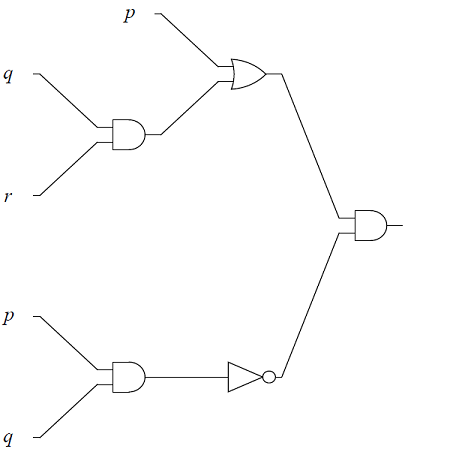
-
The logic circuit, with input variables, \(a, b\), \(c\).
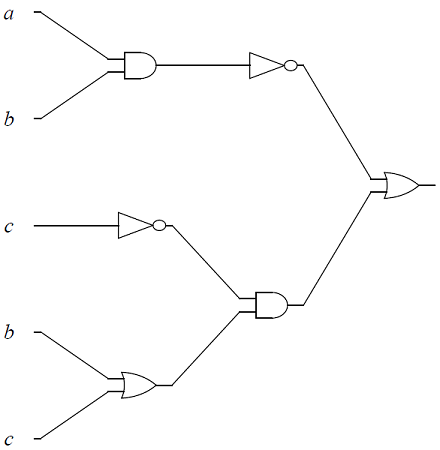
-
-
Design a logic circuit for \(r\land (p\lor (r\land \neg q))\).
4.7. Challenge Exercises
-
Complete parts (a) and (b) to show that every compound proposition is logically equivalent to one that uses the same propositional variables but only the NAND operator \(\uparrow.\)
-
For each of the three propositions \(\neg p\), \(p \land q,\) and \(p \lor q,\) write a logically equivalent proposition that uses only \(p,\) \(q,\) and \(\uparrow.\)
-
Use the theorem that every compound proposition is equivalent to a compound proposition in disjunctive normal form to justify that the compound proposition is also equivalent to one that uses only the NAND operator \(\uparrow.\)
-
-
Complete parts (a) and (b) to show that every compound proposition is logically equivalent to one that uses the same propositional variables but only the NOR operator \(\downarrow.\)
-
For each of the three propositions \(\neg p\), \(p \land q,\) and \(p \lor q,\) write a logically equivalent proposition that uses only \(p,\) \(q,\) and \(\downarrow.\)
-
Use the theorem that every compound proposition is equivalent to a compound proposition in disjunctive normal form to justify that the compound proposition is also equivalent to one that uses only the NOR operator \(\downarrow.\)
-