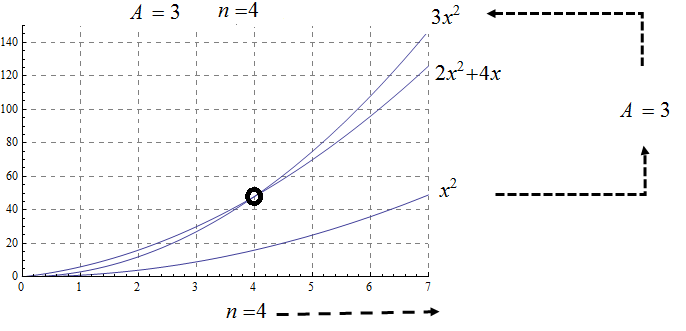12. Rates of Growth of Functions

CAUTION - CHAPTER UNDER CONSTRUCTION!

This chapter was last updated on April 14, 2025.

You have seen that some tasks can be completed by more than one algorithm. Two questions to ask are

  1. "How do you choose which algorithm to use?"

  2. "Why is is it important to make such a choice?"

This chapter will discuss tools you can use to help answer these questions. In particular, ways of comparing the rates of growth of functions will allow us to compare how two algorithms perform as the size of their input increase with no upper bound.

Key terms and concepts covered in this chapter:

  • Complexity

  • Big-\(\Theta\) notation

  • Big-\(O\) notation

12.1. Complexity of Algorithms

In order to implement an algorithm, there are issues of the space needed to do the work and the time needed to complete all the steps.

For example, imagine that you are asked to complete a few Algebra homework exercises by hand, and each exercise involves solving linear equations by hand using paper and pencil. Now suppose that "few" means "one hundred" and that each linear equation involves multiple steps to solve like the one below. \[ \text{Exercise 1. Solve for } x \text{: } 40(x+6)-9(3x+5) = 65(x+7)-(7x+132)\] It is not difficult to solve linear equations like this one because it is clear what steps you need to use…​ but it is tedious and will likely require a lot of paper! That is, it will consume a lot of time and space to solve even the first one of these equations, and you’ll have only ninety-nine more to do after that!

In this textbook, the focus will be on time complexity and asymptotics, that is, the comparison of the time needed by the algorithms as the size of the input becomes larger and larger without any bound.

12.2. The Order of a Function and Big Theta Notation

In this section, we will define a relation that describes what it means to say that "two functions grow at the same rate." More precisely, "two functions grow at the same rate, asymptotically, as the input variable grows without an upper bound." We will also introduce big \(\Theta\) notation.
Note: \(\Theta\) is the uppercase Greek letter "Theta."

Definition

Suppose that \(f\) and \(g\) are two functions, both having domain \(\mathbb{R}\) and codomain \(\mathbb{R}\). Define the relation f has the exact same order as g to mean that

There exist positive real number constants \(A,\) \(B,\) and \(x_{0}\) so that \[ A|g(x)| \leq |f(x)| \leq B|g(x)| \text{ for all } x > x_{0}.\]

The constants \(A,\) \(B,\) and \(x_{0}\) are called witnesses: The constants confirm the "has the exact same order as" relationship between the two functions.
The Remix’s definition of "has the exact same order as" is based on notations and descriptions proposed by Donald Knuth in the 1976 letter "Big Omicron and Big Omega and Big Theta" published in ACM SIGACT News .

Illustration: Two functions that have the exact same order

Consider the functions \(f\) and \(g,\) each with domain \(\mathbb{R}\) and codomain \(\mathbb{R},\) described by the rules \[ f(x) = x + \sin(x), \, g(x) = x.\] The function g is linear and the function f is not, but f can be thought of as asymptotically linear in the sense that its growth is more like that shown in a straight line plot of a linear function than, say, a parabolic plot for a quadratic function or a square root function. This is what we are describing with the relation "has the exact same order as."

Let’s plot the graphs of f and two constant multiples of g to illustrate what the relation "has the exact same order as" means.

BigThetaLinear010

The preceding image shows the plots of the graphs of the functions \(f,\) \(0.9g,\) and \(1.1g.\) Notice that for x between -10 and 10, the corresponding y output for f is sometimes between the two straight lines, sometimes above both lines, and sometimes below both lines.

BigThetaLinear010

However, if we zoom out, it appears that the plotted graph of \(f\) lies between the two straight lines for all values of the input x that have a large absolute value. In fact, the image seems to indicate that \[ 0.9g(x) \leq f(x) \leq 1.1g(x) \text{ for all } x \geq 100.\] That is, the image suggests that f has the exact same order as g. Notice that we could prove, more rigorously, that the inequality is true, by using some algebra and the fact that the sine function’s outputs are in the interval \([-1, \, 1\)], so the functions have the exact same order. The two functions \(f\) and \(g\) grow at the same rate, asymptotically, as the input variable grows without an upper bound.
It appears from the zoomed-out plot that we could choose a value less than 100 for the bound \(x_{0},\) but the definition of "has the exact same order as" does not require us to find optimal values of any of the constants \(A,\) \(B,\) and \(x_{0}.\) In fact, if there exists at least one ordered triple \(( A, \, B, \, x_{0})\) that witnesses the "has the exact same order as" relation between two functions, then there must be infinitely many other ordered triples that witness the same relationship. As an example, we’ve used the ordered triple \(( 0.9, \, 1.1, \, 100)\) for the two multipliers and the lower bound for inputs, but we could use the same two multipliers and any value greater than 100 for \(x_{0}\) instead. Also, the triple \(( \frac{1}{4}, \, 4, \, 0)\) witnesses the same relationship since \[ \frac{1}{4}g(x) \leq f(x) \leq 4g(x) \text{ for all } x \geq 0.\]

BigThetaLinear010_alt

We have the following theorem about the "has the exact same order as" relation.

Theorem

For any functions \(f,\) \(g,\) and \(h\) with domain \(\mathbb{R}\) and codomain \(\mathbb{R},\)

(1) \(f\) has the exact same order as \(f,\)
(2) if \(f\) has the exact same order as \(g,\) then \(g\) has the exact same order as \(f,\)
(3) if \(f\) has the exact same order as \(g,\) and \(g\) has the exact same order as \(h,\) then \(f\) has the exact same order as \(h.\)

Proof
For statement (1), choose any value \(x_{0}\) that is in the domain of \(f\) and \(A = 1\) and \(B = 1\) as witnesses. Since \[1 \cdot |f(x)| \leq |f(x)| \leq 1 \cdot |f(x)| \text{ for all } x \geq x_0\] must be True, \(f\) has the exact same order as \(f.\) Notice that we could have used other values for the witnesses \(A\) and \(B\) such as \(A = 0.99\) and \(B = 1.01.\)

For statement (2), assume that \(f\) has the exact same order as \(g,\) so there are positive real number constants \(A,\) \(B,\) and \(x_{0}\) such that \[A|g(x)| \leq |f(x)| \leq B|g(x)| \text{ for all } x > x_{0}.\] Notice that the extended inequality above can be broken into the two inequalities \[A|g(x)| \leq |f(x)| \text{ and } |f(x)| \leq B|g(x)|\] which are both True for all \(x > x_{0}.\) The two inequalities can be rewritten as \[|g(x)| \leq \frac{1}{A}|f(x)| \text{ and } \frac{1}{B}|f(x)| \leq |g(x)|\] which shows that \[\frac{1}{B}|f(x)| \leq |g(x)| \leq \frac{1}{A}|f(x)| \text{ for all } x > x_{0}.\] The last extended inequality above shows that \(g\) has the exact same order as \(f.\)

For statement (3), assume both that \(f\) has the exact same order as \(g\) and that \(g\) has the exact same order as \(h.\) This means that there are positive real number constants \(A,\) \(B,\) and \(x_{0}\) such that \[A|g(x)| \leq |f(x)| \leq B|g(x)| \text{ for all } x > x_{0}\] and also positive real number constants \(C,\) \(D,\) and \(x_{1}\) such that \[C|h(x)| \leq |g(x)| \leq D|h(x)| \text{ for all } x > x_{1}.\] By breaking up the extended inequalities, then doing some algebra and recombining inequalities, you can get \[AC|h(x)| \leq A|g(x)| \leq |f(x)| \text{ and } |f(x)| \leq B|g(x)| \leq BD|h(x)|\] which are True for all pass:[\(x > max(x_{0}, x_{1}).\)] So \[AC|h(x)| \leq |f(x)| \leq BD|h(x)| \text{ for all } x > max(x_{0}, x_{1})\] which shows that \(f\) has the exact same order as \(h,\) witnessed by the constants \(AC,\) \(BD,\) and \(max(x_{0}, x_{1}).\)

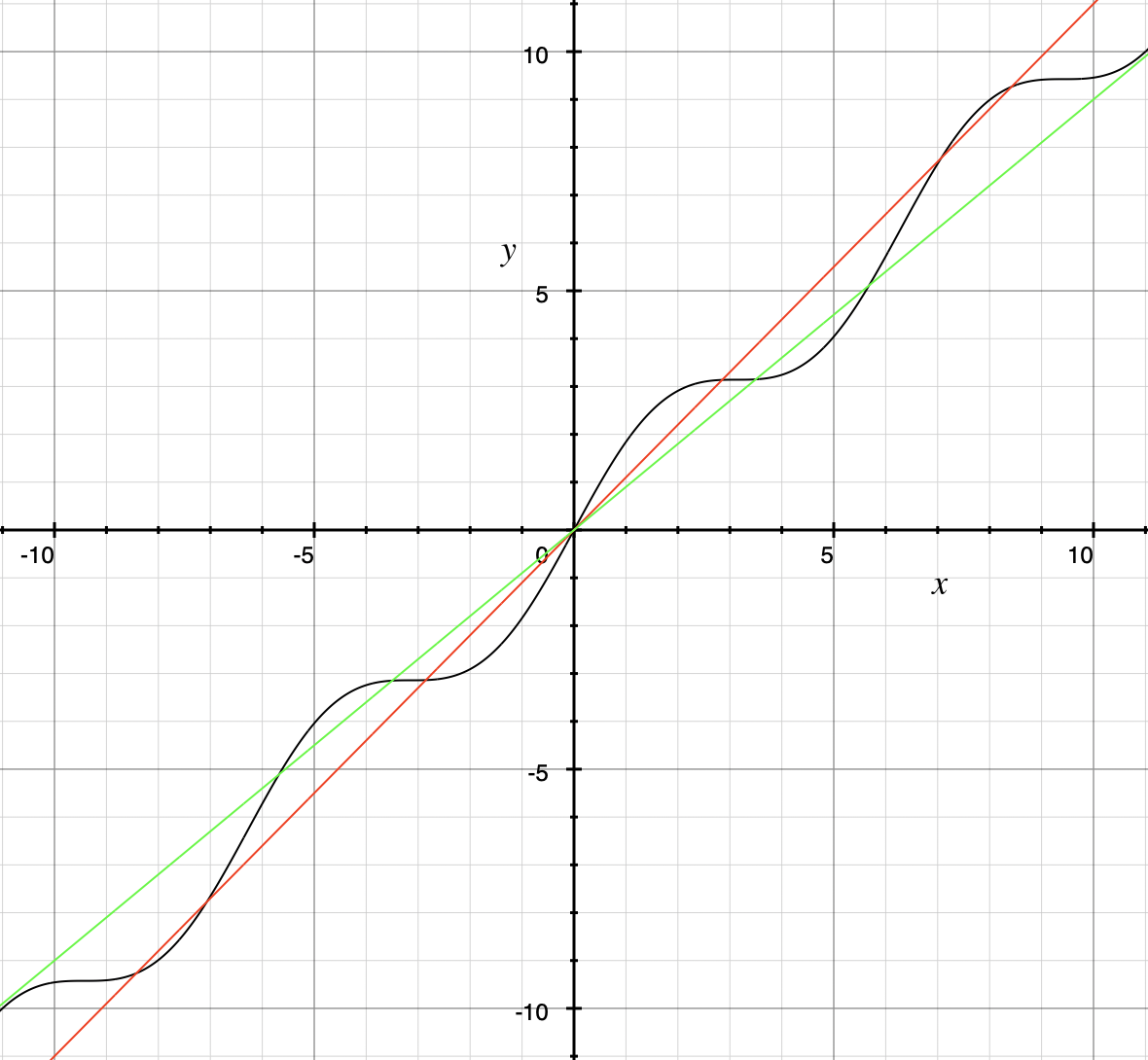
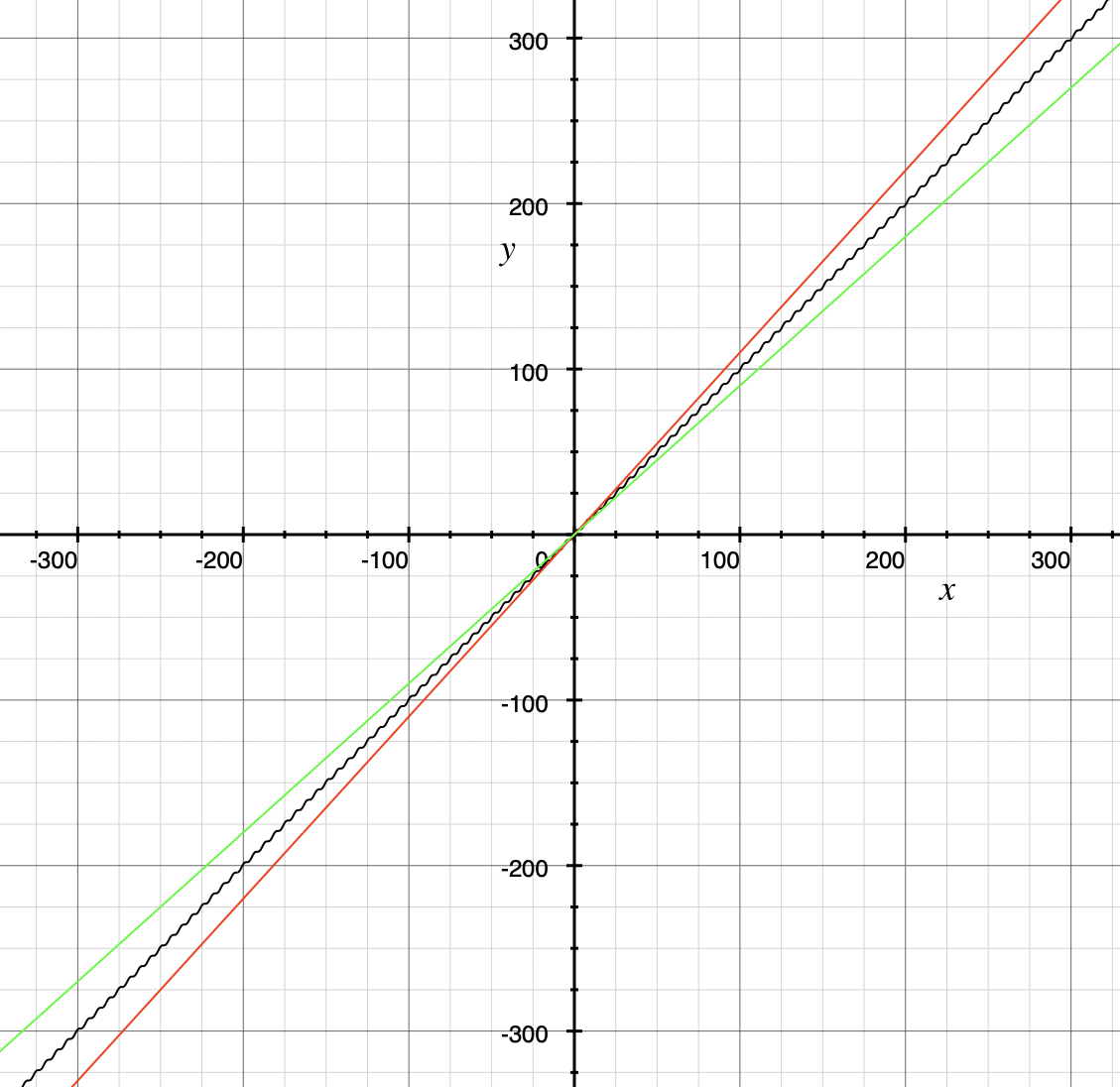
These three properties let you conclude that the "has the exact same order as" relation is an equivalence relation, so the relation partitions the set \(S = \{ f \, | \, f \text{ is a function with domain and codomain } \mathbb{R} \}\) into disjoint sets. For each function \(g \in S\) we can define \(\Theta(g)\) to be the equivalence class \[ \Theta(g) = \{ f \, | \, f \text{ has the exact same order as } g \} \] Every function with domain and codomain \(\mathbb{R}\) is an element of at least one of the \(\Theta(g)\) and for any two functions \(g\) and \(h,\) the sets \(\Theta(g)\) and \(\Theta(h)\) must either be equal or have empty intersection. For example, the earlier example shows that \(\Theta(x + \sin x)\) and \(\Theta(x)\) are the same set, so we can say that the function \(f(x) = x + \sin x\) is of linear order.

Mathematicians and computer scientists are very different beasts…​ well, they are all human but they have developed different cultures so they often use the same symbols in different ways.

A mathematician, like the author of the Remix, would write the very formal \(f \in \Theta(g)\) and state " f is an element of Theta g " to mean that " f has the exact same order as g. " In the earlier example, a mathematician could abbreviate this a little bit and write "\(x + \sin(x)\) is in \(\Theta(x).\)"

Computer scientists have traditionally written this relation as \(f(x) = \Theta(g(x))\) and state "\(f(x)\) is big Theta of \(g(x)\)." In the earlier example, a computer scientist could write "\(x + \sin(x) = \Theta(x)\)." As a mathematician, I need to point out that the function f is not equal, in the mathematical sense, to the equivalence class containing g because it’s just one of the infinitely many functions in that equivalence class.

I believe that both mathematicians and computer scientists agree that Θ( g ( x )) = f ( x ) is just too hideous a notation to use…​ so please do not ever, ever use it!

12.3. Big O notation

Traditionally, computer scientists are much more interested in the idea that " f grows at most at the rate of g ". This corresponds to the second part of the inequality used to define big Theta in the previous section.

Definition

f is of order at most g means that there exist positive real number constants \(B\) and \(x_{0}\) so that \[ |f(x)| \leq B|g(x)| \text{ for all } x > x_{0}.\] This is usually stated (by computer scientists) as "\(f(x)\) is Big O of \(g(x)\)" and written as \(f(x) = O(g(x)).\)

BigOmegaXPlusSinX

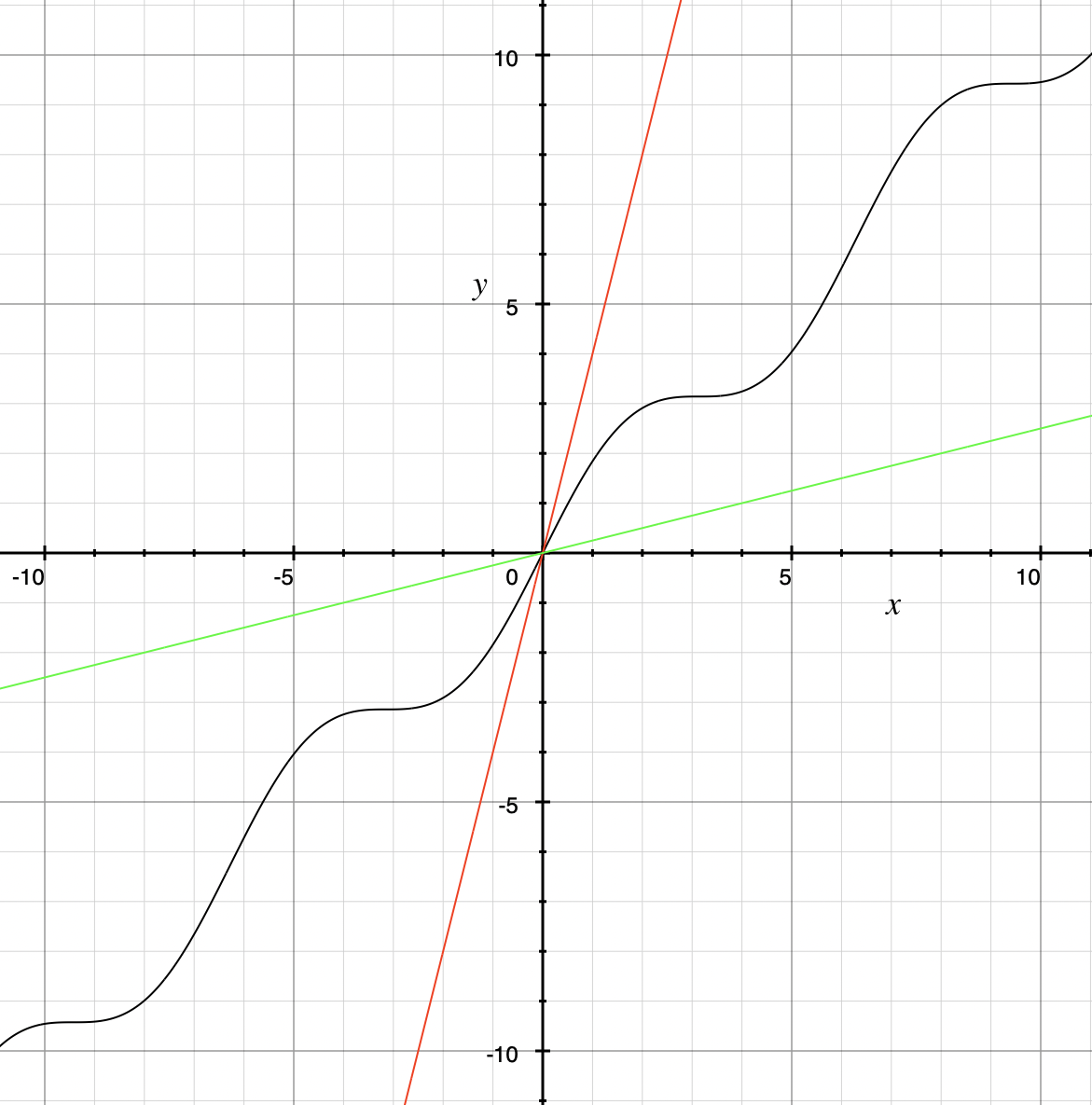
Note that Big O only gives an upper bound on the growth rate of functions. That is, the function \(f(x) = x + \sin(x)\) with domain and range \(\mathbb{R},\) used in an earlier example, is \(O(x)\) but also is \(O(x^{2})\) and is \(O(2^{x}).\)

Big O is typically used to analyze the worst case complexity of an algorithm. If, for example, \(n\) is the size of the input, then big O really only cares about what happens in the "worst-case" when \(n\) becomes arbitrarily large. Mathematically, we want to consider time complexity in this asymptotic sense, when \(n\) is arbitrarily large, so may ignore constants. That we can ignore constants will make sense after discussing how limits, borrowed from continuous mathematics (that is, calculus), can be used to compare the rates of growth of two different functions.

12.3.1. Common Complexities To Consider

The size of the input complexities most commonly used, ordered from smallest to largest, are as follows.

  • Constant Complexity: \(O(1)\)

  • Logarithmic Complexity: \(O(\log (n))\),

  • Radical complexity : \(O(\sqrt{n})\)

  • Linear Complexity: \(O(n)\)

  • Linearithmic Complexity: \(O(n\log (n))\),

  • Quadratic complexity: \(O(n^2)\)

  • Cubic complexity: \(O(n^3)\),

  • Exponential complexity: \(O(b^n)\), \( b > 1\)

  • Factorial complexity: \( O(n!)\)

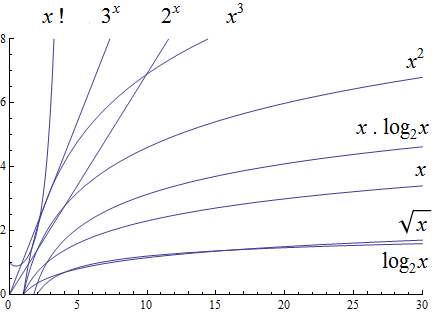
To understand the sizes of input complexities, we will look at the graphs of functions; it is easier to consider these functions as ones that are defined for any real value input instead of just the natural numbers. This will also allow us to use continuous mathematics (that is, calculus) to analyze and compare the growth of different functions.

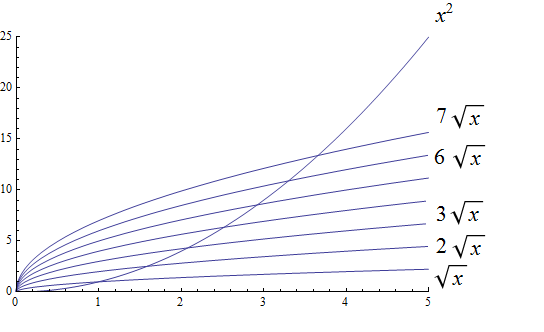
Radical growth is larger than logarithmic growth:

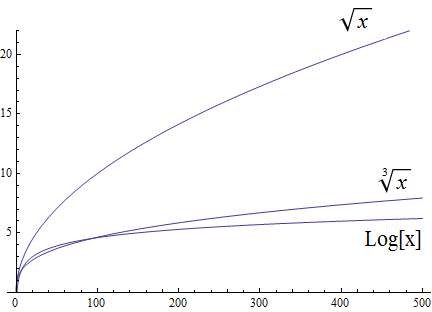
geometricsequence
In the preceding graph, we’ve used \(\text{Log}[x\)] to label the graph of a logarithmic function without stating the base for the logarithm: Is this the function \(y = log_{2}(x)\), \(y = log_{10}(x)\), \(y = ln(x) = log_{e}(x)\), or a logarithm to some other base? For the purposes of studying growth of functions, it does not matter which of these logarithms we use: You may recall that one of the properties of logarithms states that for two different positive constant bases \(a\) and \(b\) we must have \(log_{a}(x) = log_{a}(b) \cdot log_{b}(x)\), where \(log_{a}(b)\) is also a constant. As stated earlier, we may ignore constants when considering the growth of functions.

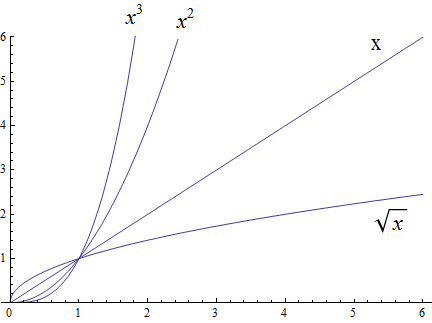
Polynomial growth is larger than radical growth:

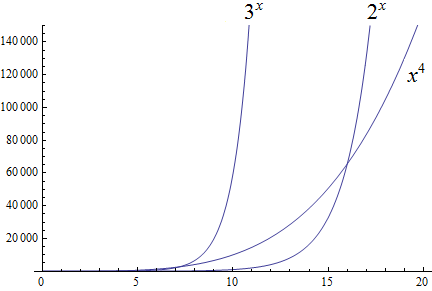
geometricsequence

Exponential growth is larger than polynomial growth:

geometricsequence

Factorial growth is larger than exponential growth:

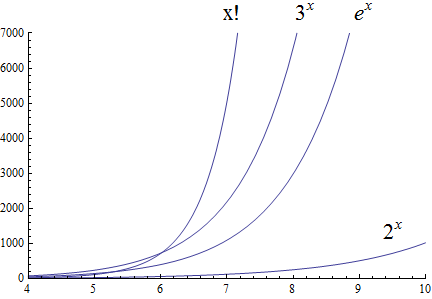
geometricsequence
In the preceding graph, we’ve used \(x!\) to label the graph of the function \(y = \Gamma(x+1)\) , where \(\Gamma\) is the Gamma function which is defined and continuous for all nonnegative real numbers. That is, \(n! = \Gamma(n+1)\) for every \(n \in \mathbb{N}\). Further study of the Gamma function is beyond the scope of this textbook.

Using the graphical analysis of the growth of typical functions we have the following growth ordering, also presented graphically on a logarithmic scale graph.

Ordering of Basic Functions by Growth
\$1,\log \ ⁡n, root(3)(n), sqrt n , n, n^2, n^3,2^n,3^n,n!, n^n\$
geometricsequence

The asymptotic behavior for large \(n\) should be determined by the most dominant term in the function for large \(n\). For example, \(f(x)=x^{3} + 2x^{2}-2x\) for large \(x\), is dominated by the term \(x^3\). In this case we want to state that \(f(x)=O(x^3)\). For example \(f(1000) =1.001998×10^9≈ 1×10^9 =1000^3\). For large \(x\), \(f(x) ≈x^3\) or asymptotically, \(f(x)\) behaves as \(x^3\) for large \(x\). We write \(f(x)=O(x^3),\) that is, \(x^3 +2x^2-2x=O(x^3).\)

Likewise we want to say that if \(c\) is a constant that \(c \cdot f(x)\), and \(f(x)\) have the same asymptotic behavior for large \(n\), or \(O(c \cdot f(x))=O(f(x))\).

Example 1

Show that \(f\left(x\right)=2x^2 +4x\) is \(O(x^2)\)

Solution

While intuitively we may understand that the dominant term for large \(x\) is \(x^2\) so that \(f(x) = O\left(x^2\right)\), we show this formally by producing as witnesses \(A=3\) and \(n =4\) with reference to the following graph.

geometricsequence
Example 2

Show that \(f(x) =2x^3 +3x\) is \(O(x^3)\), with \(A=3\) and \(n=2\). Support your answer graphically.

Solution

Notice that \( x^3 > 3x\) when \( x \geq 2\). This means \(2x^3 +x^3 > 2x^3 +3x \) when \(x >2 \). In other words \( 3x^3 > 2x^3 +3x\) whenever \( x>2\), confirming \(A=3\) and \(n=2\) as witnesses, and supported by the following graph.

geometricsequence

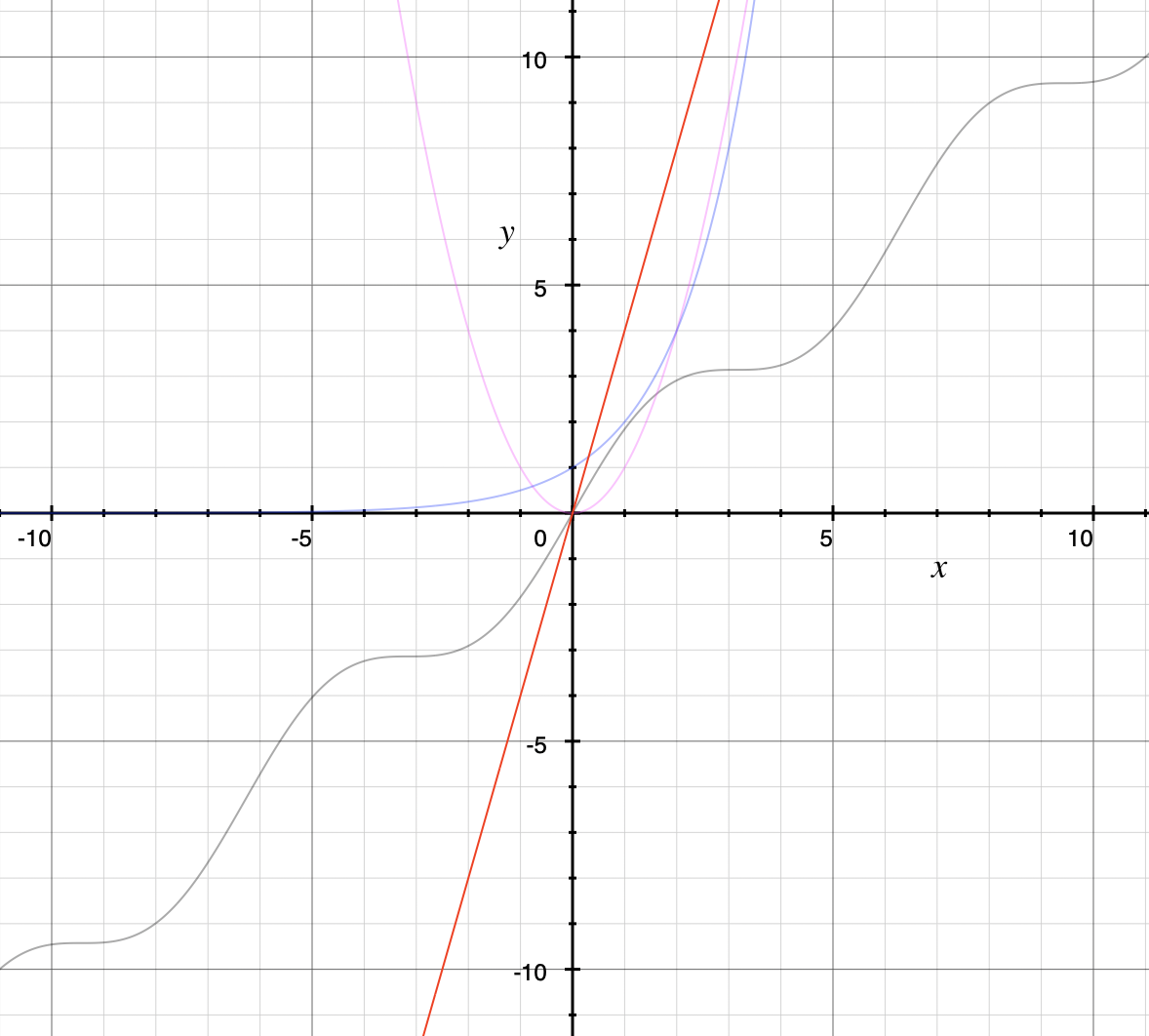
To show that a function \( f(x)\) is not \(O(g(x))\), means that no \(A\) can scale \(g(x)\) so that \( Ag(x) \geq f(x)\) for \(x\) large enough as in the following example.

Example 3

Show that \( f(x) = x^2\) is not \( O( \sqrt{x})\).

Solution

Consider the graphs of \( \sqrt{x}\), \( 2 \sqrt{x}\), \( 3\sqrt{x}\), and the graph of \(x^2\). Notice that eventually, or for \(x\) large enough, \(x^2\) is larger than any \(A \sqrt{x}\) as in the figure below

geometricsequence

Suppose \(A>1\) is given and fixed , then if \( f(x) = x^2\) is \( O(g(x))=O( \sqrt{x})\) , there is a corresponding \(n\), also fixed , for which \(A \sqrt{x} \geq x^2\) whenever \(x>n\).

We solve the inequality \(A \sqrt{x} ≥ x^2\) by dividing both sides by \(\sqrt{x} =x^{1/2}\), to obtain, \(A \sqrt{x} ≥ x^{3/2}\).

But \(A\) is fixed and cannot be greater than all arbitrarily large \( x^{3/2}\). Hence no such \(n\) can exist for a given fixed \(A\).

For example, consider \(g(x)=A \sqrt{x}\) and \( f(x) =x^2 \), when \( x= A^2\) we obtain \( g(A^2) = A \sqrt{(A^2)}= A^2\) and \( f(A^2) = {\left ( {A}^2 \right )}^2\) and \( f(A^2)= A^4 > A^2 = g(A^2) \) when \(A>1\).

12.4. Properties of Big O notation.

Suppose \(f(x)\) is \(O(F(x))\) and \(g(x)\) is \(O(G(x))\).

Properties of Big O Notation

  1. \(c \cdot f(x)\) is \(O(F(x))\)

  2. \( f (x )+g(x)\) is \(O(\max \left ( F(x), G(x) \right )\)

  3. \( f (x ) \cdot g(x))\) is \(O(F(x) \cdot G(x))\)

We can use these properties to show for instance \( 2x^2\) is \(O\left(x^2\right)\). Likewise if \(f(x) =2x^2\) and \(g(x) =4x\), then \( 2x^2\) is \(O(x^2)\) and \( 4x\) is \(O(x)\), and the maximum gives that \(2x^2+4x\) is \( O(\max(x^2, x)) =O(x^2)\).

It is true in general that if a polynomial \(f(x)\) has degree \(n\) then \(f(x)\) is \(O(x^n)\).

Big O for Polynomials

\(p(x)=a_nx^n +a_{n-1}x^{n-1} +a_{n-2}x^{n-2}+\ldots +a_2x^2 +a_1x^1+a_0\) is \(O(x^n)\)

For example, if \(f(x)= x^3+1\) being \( O(x^3)\), and \(g(x)=x^2-x\) being \(O(x^2)\), then \(f(x) \cdot g(x)\) is \(O(x^3 \cdot x^2) =O(x^5)\). This is verified explicitly by multiplying \(f(x) \cdot g(x)= (x^3+1) \cdot (x^2-x)= x^5 -x^4+x^2-x \) which clearly is \(O(x^5)\)

Example 4 - ordering by growth

Order the following functions by growth: \(n⋅\log_2⁡ n\) , \(n^2\), \(n^{4/3}\)

Solution

Recall the ordering,

\(\log_2⁡ n\), \(n^{1/3}\), and \(n\),

which is ordered by logarithmic, then radical, and then polynomial (or linear) growth.

Notice also, that multiplying each by \(n\), preserves the order.

\(n⋅\log_{2⁡}n=n\times \log_{2⁡}n\)

\(n^{4/3} =n \times n^{1/3}\)

\(n^2=n \times n\)

The using the original ordering, \(\log{n}\), \(n^{1/3}\), \(n\), we obtain also the following ordering \(n⋅\log n\), \(n^{4/3}\), \(n^2\).

As a final example we consider ordering three functions by growth using the basic properties for Big O and the basic orderings.

Example 5

Find the Big O of each of the following and then rank by Big \(O\) growth:

\(f\left(x\right)=\left({3x}^3+x\right)2^x+\left(x+x!\right)x^4\)

\(g\left(x\right)=x^x(2^x+x^2)\)

\(h\left(x\right)=5x!+4x^3\log{x}\)

Solution

First consider \(f\left(x\right)\) and using the polynomial property observe that \(\left({3x}^3+x\right)\) is \(O(x^3)\). Using the multiplicative property, conclude that \(\left({3x}^3+x\right)2^x\) is \(O(x^32^x)\). Likewise using the sum property, \(\left(x+x!\right)\) is \(O\left(\max{\left(x,x!\right)}\right)= O (x!)\). Then using the multiplicative property, \(\left(x+x!\right)x^4\) is \(O (x^4x!)\). Then \(f\left(x\right)=\left({3x}^3+x\right)2^x+\left(x+x!\right)x^4\) is \(O\left(\max{\left(x^32^x,x^4x!\right)}\right)=O\left(x^4x!\right)\).

For \(g(x)\), notice using the maximum property for the sum, that \(2^x+x^2\) is \(O(2^x)\). Then using the multiplicative property, \(x^x(2^x+x^2)\) is \(O(2^xx^x)\).

For \(h\left(x\right)\), we want \(O\left(\max{\left(x!,\ x^3\log{x}\right)}\right)=O(x!)\). Notice here, that \(4x^3\log{x}\) is \(O(x^4)\), and \(x^4\) has smaller asymptotic growth than \(x!\). In fact, \(x^4\) is \(O(x!)\).

So, \(f(x)\) is \(O\left(x^4x!\right)\), and \(g(x)\) is \(O\left(2^xx^x\right)\). Also, \(h(x)\) is, \(O\left(x!\right)\).

We conclude that from an ordering perspective, we have by increasing growth order, \(h(x)\), \(f(x)\), and \(g(x)\). To convince yourself that \(g(x)\) grows faster than \(f(x)\), use the facts that \(2^x\) grows faster than \(x^4\), and \(x^x\) grows faster than \(x!\).

12.5. Using Limits to Compare the Growth of Two Functions (CALCULUS I REQUIRED!)

In general, the Remix avoids using calculus methods because calculus is part of continuous mathematics, not discrete mathematics. However, it can be useful to use calculus to compare the growth of two functions \(f(x)\) and \(g(x)\) that are defined for real numbers \(x\), are differentiable functions on the interval \((0,\, \infty)\), and satisfy \(\lim_{x \to \infty} f(x) = \lim_{x \to \infty} g(x) = \infty\). To avoid needing to use the absolute value, we can assume that \(0 < f(x)\) and \(0 < g(x)\) for all \(x \geq 0\) (This assumption is safe to make since both functions go to infinity as \(x\) increases without bound, which means that both functions are positive for all \(x\) values greater than or equal to some number \(x_{0}\)…​ we are just assuming that \(x_{0}=0\) which is the equivalent of shifting the plots of \(f\) and \(g\) to the left by \(x_0\) units.)

If \(f(x)\) and \(g(x)\) are such functions and \(\lim_{x \to \infty} \frac{f(x)}{g(x)} = L\), where \(0 \leq L < \infty\), then \(f(x)\) is \(O(g(x)),\) and if \(0 < L < \infty\) then \(f(x)\) is \(\Theta(g(x)).\)

To see this, recall that \(\lim_{x \to \infty} \frac{f(x)}{g(x)} = L\) means that we can make the value of \(\frac{f(x)}{g(x)}\) be as close to \(L\) as we want by choosing \(x\) values that are sufficiently large. In particular, we can make \(L-\frac{L}{2} < \frac{f(x)}{g(x)} < L+\frac{L}{2}\) be true for all \(x\) greater than some real number \(x_{0}\). Now we can use the earlier stated assumption that \(0 \leq g(x)\) to rewrite the inequality as \((L-\frac{L}{2}) \cdot g(x) < f(x) < (L+\frac{L}{2}) \cdot g(x)\), which is true for all \(x >x_{0}\). We can choose for our witnesses \(B = L + \frac{L}{2}\) and \(x_{0}.\) This means that \(f(x) < B \cdot g(x)\) whenever \(x > x_{0},\) which shows that \(f(x)\) is \(O(g(x))\). Furthermore, if \(L>0\) we can choose \(A = L - \frac{L}{2}\) as a witness for the lower bound, too, which means that \( A \cdot g(x) < f(x) < B \cdot g(x)\) whenever \(x > x_{0},\) so \(f(x)\) is \(\Theta(g(x))\).

Note that using this method does not focus on determining the actual numerical values of \(A\) and \(n\) but just guarantees that the witnesses exist, which is all that is needed to show that \(f(x)\) is \(O(g(x))\).

Example 6

Show that \(100,000 n + n \cdot log (n)\) is \(O(n \cdot log (n))\).

Solution

Notice that the expressions \(100,000 x + x \cdot log (x)\) and \(x \cdot log (x)\) can be used to define differentiable functions on the interval \((0,\, \infty)\). We changed the variable from \(x\) to \(n\) to stress that we are treating the variable as a real number in this example. Also, we will assume that \(log (x)\) is the natural logarithm; as mentioned earlier, any other base for the logarithm results in a constant multiple of the natural logarithm and will not effect the Big-\(O\) computations.

Let \(f(x) = 100,000 x + x \cdot log (x)\) and \(g(x) = x \cdot log (x)\). It is easy to see that \(\lim_{x \to \infty} f(x) = \lim_{x \to \infty} g(x) = \infty\).

Now let’s compute \(\lim_{x \to \infty} \frac{f(x)}{g(x)}\), that is, \(\lim_{x \to \infty} \frac{100,000 x + x \cdot log(x)}{x \cdot log (x)}\). Direct computation gives the indeterminate form \(\frac{\infty}{\infty}\), so we can use L’Hôpital’s rule to write \(\lim_{x \to \infty} \frac{100,000 x + x \cdot log(x)}{x \cdot log(x)} = \lim_{x \to \infty} \frac{100,000 + (1 \cdot log (x) + x \cdot \frac{1}{x})}{1 \cdot log(x) + x \cdot \frac{1}{x}} = \lim_{x \to \infty} \frac{100,000 + log (x) + 1}{log(x) + 1}\). This limit still gives us an indeterminate form if we try to directly find the limits of the numerator and denominator separately without some simplification, but we can divide both numerator and denominator by \(log (x)\) to rewrite the last limit as the equivalent limit \(\lim_{x \to \infty} \frac{\frac{100,001}{log (x)} + 1}{1 + \frac{1}{log(x)}} = \frac{0+1}{1+0} = 1\). Since the limit is a positive finite number, \(100,000 x + x \cdot log (x)\) is \(\Theta(x \cdot log (x))\) which means that is also \(O(x \cdot log (x)).\) As mentioned above, we do not need to find the actual values of the witnesses when using this limit method.

12.6. Exercises

  1. Give Big O estimates for

    1. \(f\left(x\right)=4\)

    2. \(f\left(x\right)=3x-2\)

    3. \(f\left(x\right)=5x^6-4x^3+1\)

    4. \(f\left(x\right)=2\ \ \sqrt x+5\)

    5. \(f\left(x\right)=x^5+4^x\)

    6. \(f\left(x\right)=x\log{x}+3x^2\)

    7. \(f\left(x\right)=5{x^2e}^x+4x!\)

    8. \(f\left(x\right)=\displaystyle \frac{x^6}{x^2+1}\) (Hint: Use long division.)

  2. Give Big O estimates for

    1. \(f\left(x\right)=2^5\)

    2. \(f\left(x\right)=5x-2\)

    3. \(f\left(x\right)=5x^8-4x^6+x^3\)

    4. \(f\left(x\right)=\) \$4 root(3)(x)+3\$

    5. \(f\left(x\right)=3^x+4^x\)

    6. \(f\left(x\right)=x^2\log{x}+5x^3\)

    7. \(f\left(x\right)=5{x^610}^x+4x!\)

    8. \(f\left(x\right)=\displaystyle \frac{x^5+2x^4-x+2}{x+2}\) (Hint: Use long division.)

  3. Show, using the definition, that \(f\left(x\right)=3x^2+5x\) is \(O(x^2)\) with \(A=4\) and \(n=5\). Support your answer graphically.

  4. Show, using the definition, that \(f\left(x\right)=x^2+6x+2\) is \(O(x^2)\) with \(A=3\) and \(n=6\). Support your answer graphically.

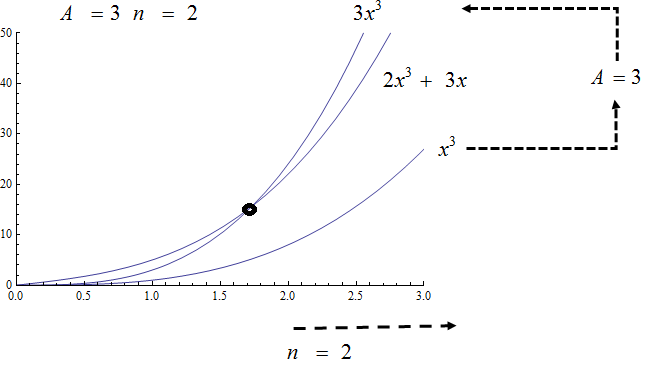
  5. Show, using the definition, that \(f\left(x\right)=2x^3+6x^2+3\) is \(O(x^2)\). State witnesses \(A\) and \(n\), and support your answer graphically.

  6. Show, using the definition, that \(f\left(x\right)=\ {3x}^3+10x^2+1000\) is \(O(x^2)\). State the witnesses \(A\) and \(n\), and support your answer graphically.

  7. Show that \(f\left(x\right)=\sqrt x\) is \(O\left(x^3\right)\), but \(g\left(x\right)=x^3\) is not\(\ O(\ \sqrt x)\).

  8. Show that \(f\left(x\right)= x^2\) is \(O\left(x^3\right)\), but \(g\left(x\right)=x^3\) is not\(\ O( x^2)\).

  9. Show that \(f\left(x\right)=\sqrt x\) is \(O\left(x\right)\), but \(g\left(x\right)=x\) is not\(\ O(\ \sqrt x)\).

  10. Show that \(f\left(x\right)=\) \$root(3)(x)\$ is \(O\left(x^2\right)\), but \(g\left(x\right)=x^2\) is not \$O( root(3)(x))\$

  11. Show that \(f\left(x\right)=\) \$root(3)(x)\$ is \(O\left(x\right)\), but \(g\left(x\right)=x\) is not \$root(3)(x)\$.

  12. Order the following functions by growth \(x^\frac{7}{3},\ e^x,\ 2^x,\ x^5,\ 5x+3,\ 10x^2+5x+2,\ x^3,\log{x,\ x^3\log{x}}\)

  13. Order the following functions by growth from slowest to fastest. \(\ 3x!,\ {10}^x,\ x\cdot\log{x},\ \log{x\cdot\log{x,\ \ }2x^2+5x+1,\ \pi^x,x^\frac{3}{2}\ },\ 4^5,\ \ \sqrt{x\ }\cdot\log{x}\)

  14. Consider the functions \(f\left(x\right)=2^x+2x^3+e^x\log{x}\) and \(g\left(x\right)=\sqrt x+x\log{x}\). Find the best big \(O\) estimates of

    1. \((f+g)(x)\)

    2. \((f\cdot\ g)(x)\)

  15. Consider the functions \(f\left(x\right)=2x+3x^3+5\log{x}\) and \(g\left(x\right)=\sqrt x+x^2\log{x}\). Find the best big \(O\) estimates of

    1. \((f+g)(x)\)

    2. \((f\cdot\ g)(x)\)

  16. State the definition of "\( f(x)\) is \( O(g(x))\)"" using logical quantifiers and witnesses \(A\) and \(n\).

  17. Negate the definition of "\( f(x)\) is \( O(g(x))\)" using logical quantifiers, and then state in words what it means that \( f(x)\) is not \( O(g(x))\).